pulsewidth
Bilevel waveform pulse width
Syntax
Description
[ returns w,initcross,finalcross]
= pulsewidth(___)finalcross, the
mid-reference level instants of the final transition of each pulse.
[ returns the waveform value w,initcross,finalcross,midlev]
= pulsewidth(___)midlev that
corresponds to the mid-reference level.
W = pulsewidth(___,Name,Value)Name,Value arguments.
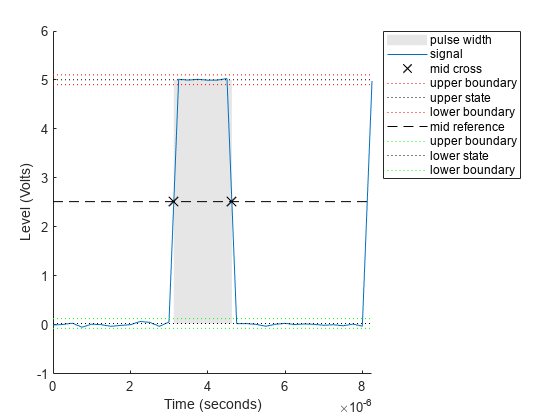
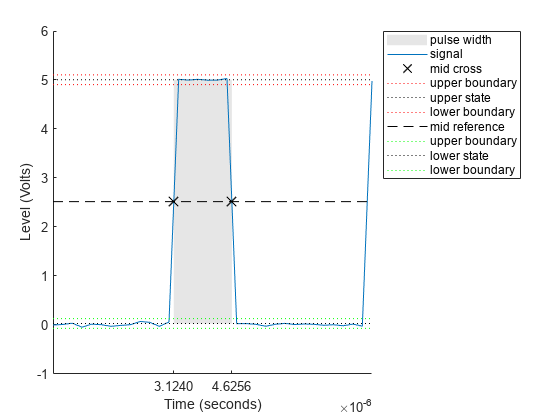
pulsewidth(___) plots the signal and darkens the regions of
each pulse where the function computes the pulse width. The function marks the location of the
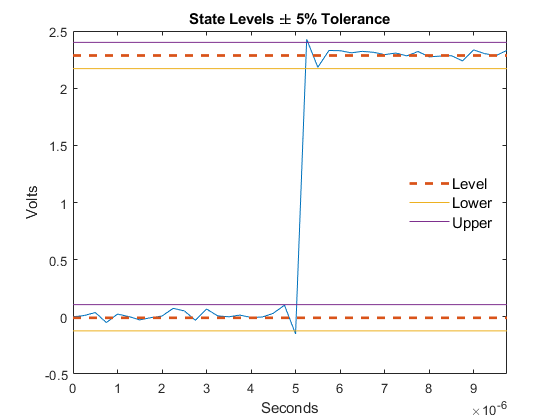
midcrossings and their associated reference level. The function also plots the state levels and
their associated lower and upper boundaries.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] IEEE Standard 181. IEEE® Standard on Transitions, Pulses, and Related Waveforms (2003).
Extended Capabilities
Version History
Introduced in R2012a