Filter
Model RF Filter
Libraries:
RF Blockset /
Circuit Envelope /
Elements
Description
The Filter block models RF filters of four designs:
Butterworth — Butterworth filters have a magnitude response that is maximally flat in the passband and monotonic overall. This smoothness comes at the price of decreased roll-off steepness.
Chebyshev — Chebyshev Type I filters have ripples of equal magnitude in the passband and monotonic in the stopband.
Inverse Chebyshev — Chebyshev Type II filters have ripples of equal magnitude in the stopband and monotonic in the passband.
Ideal — Ideal filters perfectly allow frequencies in the passband and completely reject frequencies in the stopband.
To filter RF complex baseband signals in Simulink, use the Idealized Baseband Filter block.
Examples
Parameters
Main
Simulation type, specified as one of the following:
Ideal— Simulates an ideal filter of the type specified in Filter type and the model specified in Implementation.Butterworth— Simulates a Butterworth filter of the type specified in Filter type and the model specified in Implementation.Chebyshev— Simulates a Chebyshev filter of the type specified in Filter type and the model specified in Implementation.Inverse Chebyshev— Simulates a inverse Chebyshev filter of the type specified in Filter type and theTransfer functionmodel specified in Implementation.
Filter type, specified as one of the following:
Lowpass— Simulates a lowpass filter type of the design specified in Design method.Highpass— Simulates a highpass filter type of the design specified in Design method.Bandpass— Simulates a bandpass filter type of the design specified in Design method.Bandstop— Simulates a bandstop filter type of the design specified in Design method.
Implementation, specified as one of the following:
LC Tee— Model an analog filter with an LC lumped Tee structure when the Design method is Butterworth or Chebyshev.LC Pi— Model an analog filter with an LC lumped Pi structure when the Design method is Butterworth or Chebyshev.Transfer Function— Model an analog filter using two-port S-parameters when the Design method is Butterworth or Chebyshev.Constant per carrier— Model a filter with either full transmission or full reflection set as constant throughout the entire envelope band around each carrier.The Design method is specified as ideal.Frequency Domain— Model a filter using convolution with an impulse response. The Design method is specified as ideal. The impulse response is computed independently for each carrier frequency to capture the ideal filtering response. When a transition between full transmission and full reflection of the ideal filter occurs within the envelope band around a carrier, the frequency-domain implementation captures this transition correctly up to a frequency resolution specified in Impulse response duration.
By default, the Implementation is
Constant per carrier for an ideal filter
and LC Tee for Butterworth or Chebyshev.
Note
Due to causality, a delay of half the impulse response duration is included for both reflected and transmitted signals. This delay will impair the filter performance when the source and load resistances differ from the values specified as filter parameters.
Passband edge frequency, specified as a scalar in Hz, kHz, MHz, or GHz.
Dependencies
To enable this parameter, set Design method
to Ideal.
Select this parameter to implement the filter order manually.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Filter order, specified as a scalar within the range between [2, 60].
This order is the number of lumped storage elements in
lowpass or highpass. In
bandpass or bandstop, the
number of lumped storage (L and C) elements are twice the value.
Note
For even order Chebyshev filters, the resistance ratio for Tee network implementation and for Pi network implementation.
where:
Rp is the passband ripple in dB.
Dependencies
To enable this parameter, select Implement using filter order.
Passband frequency for low[pass and highpass filters specified as a scalar in Hz, kHz, MHz, or GHz. Based on the Filter type you select, the default value of this parameter varies. The default values are listed in this table.
| Filter Type | Default value of passband frequency |
|---|---|
Lowpass | 1 GHz
|
Highpass | 2 GHz
|
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Lowpass , or
Highpass.
Passband frequencies for bandpass filters, specified as a 2-tuple vector in Hz, kHz, MHz, or GHz. This option is not available for bandstop filters.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Bandpass.
Passband attenuation, specified as a scalar dB. For bandpass filters, this value is applied equally to both edges of the passband.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Stopband frequencies for bandstop filters, specified as a 2-tuple vector in Hz, kHz, MHz, or GHz. This option is not available for bandpass filters.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Bandstop.
Stopband attenuation, specified as a scalar dB. For bandstop filters, this value is applied equally to both edges of the stopband.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Bandstop.
Input source resistance, specified as a scalar in ohms.
Note
The source and load impedances must be equal when
Implementation is set to
Transfer function.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Output load resistance, specified as a scalar in ohms.
Note
The source and load impedances must be equal when
Implementation is set to
Transfer function.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Select to internally ground and hide the negative terminals. Clear to expose the negative terminals. When the terminals are exposed, you can connect them to other parts of your model.
Use this button to save filter design to a MAT or TXT file. For more information, see Export Your Filter Design.
Visualization
Type of plots, specified as Voltage
transfer, Phase delay, or
Group delay.
Type of plots, specified as None,
Voltage transfer, Phase
delay, or Group
delay.
Scaling of y-axis, specified as,
Magnitude(decibels),Magnitude(linear)orAngle(degrees),Real, orImaginaryforVoltage transferparameters.Magnitude(decibels)orMagnitude(linear)forPhase delayorGroup delayparameters.
Scaling of y-axis, specified as,
Magnitude(decibels),Magnitude(linear)orAngle(degrees),Real, orImaginaryforVoltage transferparameters.Magnitude(decibels)orMagnitude(linear)forPhase delayorGroup delayparameters.
Frequency points to plot on x-axis, specified as a vector with each element units in Hz, kHz, MHz, or GHz.
X-axis scale, specified as Linear or
Logarithmic.
Y-axis scale, specified as Linear or
Logarithmic.
More About
By clicking the Export button, you can export your filter design to a MAT or TXT file. You can then load this file and view the block parameters, as well as the resulting capacitor and inductor element values, which are stored as variables.
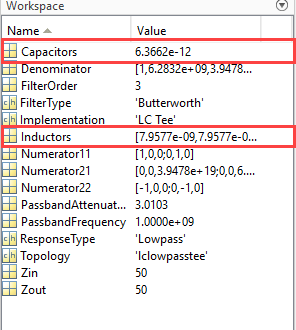
You can also view the resulting element values connected in an LC Tee or LC Pi
ladder network topology. To view the element values, right-click the
Filter block and select Mask, and then
Look Under Mask. Pause on or click the element to see
its label. You can map the resulting element values, stored in the MAT file as
Capacitors and Inductors variables, to the
elements connected in this ladder network using the labels.

To design an LC Tee or LC Pi ladder network, use the Implementation parameter.
| Filter Type | Frequency Response |
|---|---|
| Lowpass |
|
| Highpass |
|
| Bandpass |
|
| Bandstop |
|

This table shows all the parameters required to design each filter correctly:

Some additional design tips:

References
[1] Kendall Su, Analog Filters, Second Edition.
[2] Louis Weinberg, Network Analysis and Synthesis, Huntington, New York: Robert E. Krieger Publishing Company, 1975.
[3] Larry D. Paarmann, Design and Analysis of Analog Filters, A Signal Processing Perspective with MATLAB® Examples, Kluwer Academic Publishers, 2001.
[4] Michael G. Ellis, SR., Electronic Filter Analysis and Synthesis, Norwood, MA: Artech House, 1994.
[5] Anatol I. Zverev, Handbook of Filter Synthesis, Hoboken, NJ: John Wiley & Sons, 2005.
Version History
Introduced in R2016b
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)





