boxchart

Box chart (box plot) for analysis of variance (ANOVA)

Since R2022b

Syntax

boxchart(aov)

boxchart(aov,factors)

boxchart(___,Name=Value)

boxchart(ax,___)

b = boxchart(___)

Description

boxchart(aov) creates a notched box plot of the response data for each factor value of the one-way anova object aov. This syntax is supported only if the factor is categorical.

boxchart(aov,factors) creates a notched box plot for each value of the factors in factors. The argument factors must consist of up to two of the categorical factor names in aov.FactorNames.

boxchart(___,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in the previous syntaxes. For example, you can specify the box median line color and the marker style. For a list of properties, see BoxChart Properties.

boxchart(ax,___) plots the axes specified by ax instead of into the current axes (gca).

b = boxchart(___) returns a graphics vector b of BoxChart objects for the generated box plots.

Examples

Plot Data for One-Way ANOVA

Load popcorn yield data.

load popcorn.mat

The columns of the 6-by-3 matrix popcorn contain popcorn yield observations in cups for three different brands.

Perform a one-way ANOVA to test the null hypothesis that the popcorn yield is not affected by the brand of popcorn.

aov = anova(popcorn,FactorNames="Brand")

aov = 
1-way anova, constrained (Type III) sums of squares.

Y ~ 1 + Brand

             SumOfSquares    DF    MeanSquares     F        pValue  
             ____________    __    ___________    ____    __________

    Brand       15.75         2        7.875      18.9    7.9603e-05
    Error        6.25        15      0.41667                        
    Total          22        17                                     


  Properties, Methods

The small p-value indicates that at least one brand has a different popcorn yield that is statistically significant.

Create a box plot of the response data for each value of Brand.

boxchart(aov)
xlabel("Brand")
ylabel("Popcorn Yield")

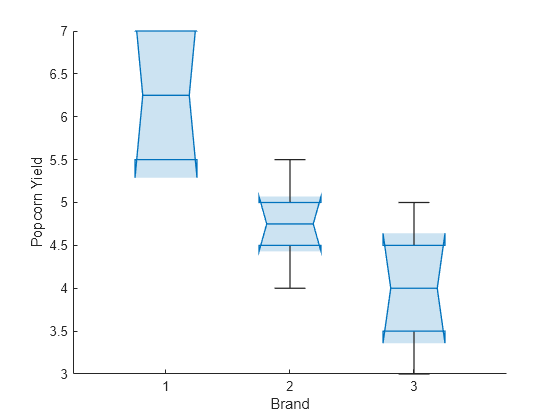
The shaded region of the first box plot does not overlap with the shaded regions of the other box plots, indicating that the difference in popcorn yield for the first brand is statistically significant.

Plot Data for Two-Way ANOVA

Load popcorn yield data.

load popcorn.mat

The columns of the 6-by-3 matrix popcorn contain popcorn yield observations in cups for the brands Gourmet, National, and Generic. The first three rows of the matrix correspond to popcorn that was popped with an oil popper, and the last three rows correspond to popcorn that was popped with an air popper.

Create string arrays containing factor values for the brand and popper type by using the repmat function.

brand = [repmat("Gourmet",6,1);repmat("National",6,1);repmat("Generic",6,1)];
poppertype = [repmat("Air",3,1);repmat("Oil",3,1);repmat("Air",3,1);...
    repmat("Oil",3,1);repmat("Air",3,1);repmat("Oil",3,1)];
factors = {brand,poppertype};

Perform a two-way ANOVA to test the null hypothesis that the popcorn yield is not affected by the brand of popcorn, type of popper, or the interaction between the brand and type of popper.

aov = anova(factors,popcorn(:),FactorNames=["Brand","PopperType"],...
    ModelSpecification="interactions")

aov = 
2-way anova, constrained (Type III) sums of squares.

Y ~ 1 + Brand*PopperType

                        SumOfSquares    DF    MeanSquares     F        pValue  
                        ____________    __    ___________    ____    __________

    Brand                    15.75       2        7.875      56.7     7.679e-07
    PopperType                 4.5       1          4.5      32.4    0.00010037
    Brand:PopperType      0.083333       2     0.041667       0.3       0.74622
    Error                   1.6667      12      0.13889                        
    Total                       22      17                                     


  Properties, Methods

aov is an anova object that contains the results of the two-way ANOVA. The small p-values for Brand and PopperType indicate that both the brand and type of popper have a statistically significant effect on the popcorn yield. The large p-value for Brand:PopperType indicates that not enough evidence exists to reject the null hypothesis that the interaction term does not have a statistically significant effect on the popcorn yield.

Use boxchart to plot the response data grouped by the values for Brand and the response data grouped by PopperType. To see the color boxchart assigns to each popper type, add a legend.

boxchart(aov,["Brand","PopperType"])
legend

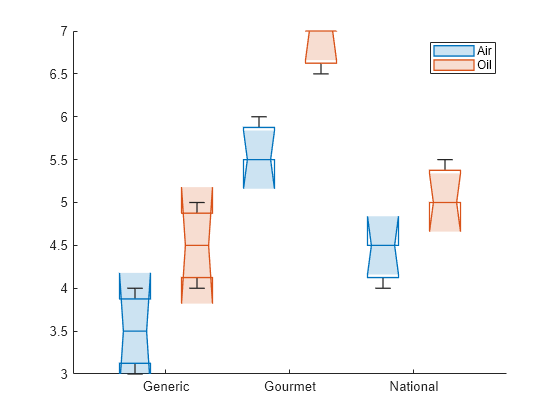
The box plots indicate that the popcorn yield is higher for popcorn popped in oil, regardless of the brand. For each type of popper, the Gourmet brand yields the most popcorn and the Generic brand yields the least. This result is consistent with the results from the two-way ANOVA.

Specify Axes for Box Plots

Load popcorn yield data.

load popcorn.mat

The columns of the 6-by-3 matrix popcorn contain popcorn yield observations in cups for the brands Generic, Gourmet, and National. The first three rows of the matrix correspond to popcorn that was popped with an oil popper, and the last three rows correspond to popcorn that was popped with an air popper.

Create string arrays containing factor values for the brand and popper type using the function repmat.

brand = [repmat("Gour.",6,1);repmat("Nat.",6,1);repmat("Gen.",6,1)];
poppertype = [repmat("Air",3,1);repmat("Oil",3,1);repmat("Air",3,1);...
    repmat("Oil",3,1);repmat("Air",3,1);repmat("Oil",3,1)];

Perform a two-way ANOVA to test the null hypothesis that the popcorn yield is not affected by the brand of popcorn or type of popper.

aov = anova({brand,poppertype}, popcorn(:), FactorNames=["Brand","PopperType"]);

Create a 1-by-2 tiled chart layout. In the first set of axes, plot the box plots for the brand. In the second set of axes, plot the box plots for the popper type.

tiledlayout(1,2)

% Left axes
ax1 = nexttile;
boxchart(ax1,aov,"Brand")
xlabel(ax1,"Brand")
ylabel(ax1,"Popcorn Yield")

% Right axes
ax2 = nexttile;
boxchart(ax2,aov,"PopperType")
xlabel(ax2,"Popper Type")

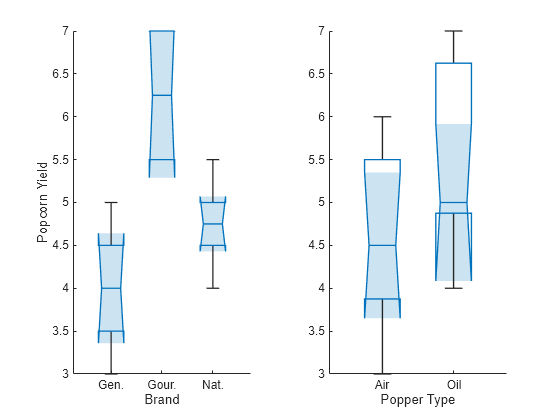
The box plot median lines indicate that the brand of popcorn has a larger effect on the popcorn yield than the type of popper.

Set Box Median Line and Face Color

Load popcorn yield data.

load popcorn.mat

The columns of the 6-by-3 matrix popcorn contain popcorn yield observations in cups for three different brands.

Perform a one-way ANOVA to test the null hypothesis that the popcorn yield is not affected by the brand of popcorn.

aov = anova(popcorn,FactorNames="Brand")

aov = 
1-way anova, constrained (Type III) sums of squares.

Y ~ 1 + Brand

             SumOfSquares    DF    MeanSquares     F        pValue  
             ____________    __    ___________    ____    __________

    Brand       15.75         2        7.875      18.9    7.9603e-05
    Error        6.25        15      0.41667                        
    Total          22        17                                     


  Properties, Methods

Plot the response data for the different values of Brand. Plot the median line in red, the box face in gray, and the box edges in black.

boxchart(aov,BoxFaceAlpha=0.2,BoxFaceColor="k",...
    BoxEdgeColor="k",BoxMedianLineColor="r")
xlabel("Brand")
ylabel("Popcorn Yield")

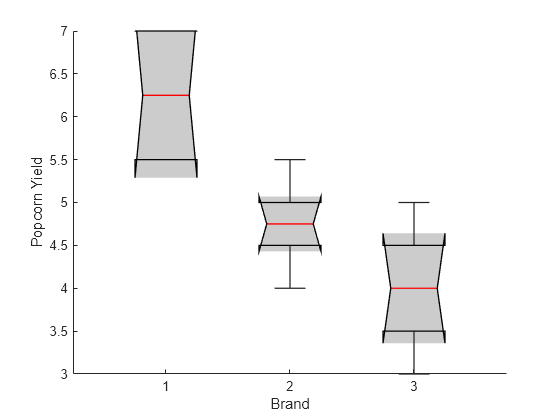
The shaded region of the first box plot does not overlap with the shaded regions of the other box plots, indicating that the difference in the popcorn yield for the first brand is statistically significant.

Input Arguments

aov — Analysis of variance results

anova object

Analysis of variance results, specified as an anova object. The properties of aov contain the factors and response data used by boxchart to generate the box plots.

factors — Factors used to group response data

string vector | cell array of character vectors

Factors used to group the response data, specified as a string vector or cell array of character vectors. The boxchart function groups the response data by the combinations of values for factors in factors. The factors input argument must be one or two of the categorical factor names in aov.FactorNames.

Example: ["g1","g2"]

Data Types: string | cell

ax — Target axes

Axes object

Target axes, specified as an Axes object. If you do not specify the axes, then boxchart uses the current axes (gca).

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: Orientation="horizontal",BoxMedianLineColor="r",WhiskerLineStyle="--" creates horizontal box plots with red median lines and dashed whiskers.

The BoxChart properties listed here are only a subset. For a complete list, see BoxChart Properties.

BoxFaceColor — Box color

RGB triplet | hexadecimal color code | color name | short name

Box color, specified as an RGB triplet, hexadecimal color code, color name, or short name. The box includes the box edges and median line. To specify the color of the box edges and median line separately, you can use the BoxEdgeColor property. To specify the color of the median line only, use the BoxMedianLineColor property.

For a custom color, specify an RGB triplet or a hexadecimal color code.

• An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1]; for example, [0.4 0.6 0.7].

• A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Thus, the color codes "#FF8800", "#ff8800", "#F80", and "#f80" are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.

Color Name	Short Name	RGB Triplet	Hexadecimal Color Code	Appearance
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"
"none"	Not applicable	Not applicable	Not applicable	No color

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB^® uses in many types of plots.

RGB Triplet	Hexadecimal Color Code	Appearance
[0 0.4470 0.7410]	"#0072BD"
[0.8500 0.3250 0.0980]	"#D95319"
[0.9290 0.6940 0.1250]	"#EDB120"
[0.4940 0.1840 0.5560]	"#7E2F8E"
[0.4660 0.6740 0.1880]	"#77AC30"
[0.3010 0.7450 0.9330]	"#4DBEEE"
[0.6350 0.0780 0.1840]	"#A2142F"

Example: BoxFaceColor="red"

Example: BoxFaceColor=[0 0.5 0.5]

Example: BoxFaceColor="#EDB120"

MarkerStyle — Outlier style

"o" (default) | "+" | "*" | "." | "x" | ...

Outlier style, specified as one of the options listed in this table.

Marker	Description	Resulting Marker
"o"	Circle
"+"	Plus sign
"*"	Asterisk
"."	Point
"x"	Cross
"_"	Horizontal line
"|"	Vertical line
"square"	Square
"diamond"	Diamond
"^"	Upward-pointing triangle
"v"	Downward-pointing triangle
">"	Right-pointing triangle
"<"	Left-pointing triangle
"pentagram"	Pentagram
"hexagram"	Hexagram
"none"	No markers	Not applicable

Example: MarkerStyle="x"

Example: MarkerStyle="none"

JitterOutliers — Outlier marker displacement

"off" (default) | "on" | true or 1 | false or 0

Outlier marker displacement, specified as "on" or "off", or as numeric or logical 1 (true) or 0 (false). A value of "on" is equivalent to true, and "off" is equivalent to false. So, you can use the value of this property as a logical value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

If you set the JitterOutliers property to "on", then boxchart randomly displaces the outlier markers along the XData direction to help you distinguish between outliers that have similar aov.Y values. For an example, see Visualize and Find Outliers.

Example: JitterOutliers="on"

Notch — Median comparison display

"off" (default) | "on" | true or 1 | false or 0

Median comparison display, specified as "on" or "off", or as numeric or logical 1 (true) or 0 (false). A value of "on" is equivalent to true, and "off" is equivalent to false. So, you can use the value of this property as a logical value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

If you set the Notch property to "on", then boxchart creates a tapered, shaded region around each median. Box plots whose notches do not overlap have different medians at the 5% significance level. For more information, see Box Chart (Box Plot).

Notches can extend beyond the lower and upper quartiles.

Example: Notch="off"

Orientation — Orientation of box plots

"vertical" (default) | "horizontal"

Orientation of box plots, specified as "vertical" or "horizontal". By default, box plots have a vertical orientation, so that the maov.Y statistics are aligned with the y-axis. Regardless of the orientation, boxchart stores the maov.Y values in the YData property of the BoxChart object.

Example: Orientation="horizontal";

Output Arguments

b — Box plots

vector of BoxChart objects

Box plots, returned as a vector of BoxChart objects. If the factors input argument contains only one categorical factor name, b contains a single BoxChart object. If factors contains two categorical factor names, b contains the same number of BoxChart objects as the number of values for the second factor. Use b to set properties of the box plots after creating them. For more information see BoxChart Properties.

Version History

Introduced in R2022b