SilhouetteEvaluation
Silhouette criterion clustering evaluation object
Description
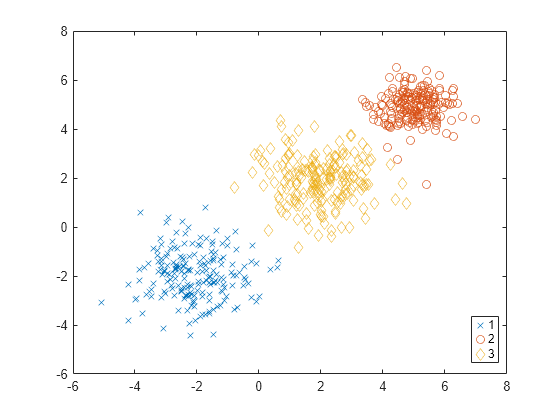
SilhouetteEvaluation is an object consisting of sample data
(X), clustering data (OptimalY), and silhouette criterion
values (CriterionValues) used to
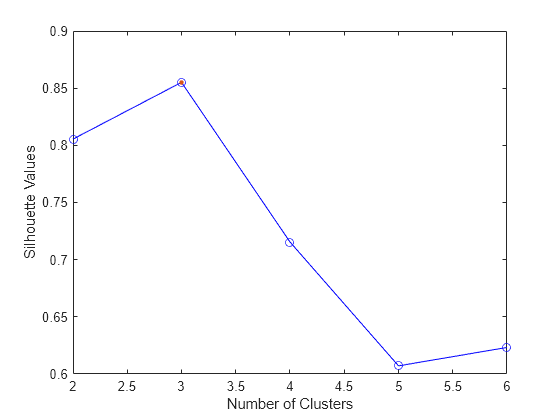
evaluate the optimal number of data clusters (OptimalK). The silhouette value for
each point (observation in X) is a measure of how similar that point is to
other points in the same cluster, compared to points in other clusters. If most points have a
high silhouette value, then the clustering solution is appropriate. If many points have a low
or negative silhouette value, then the clustering solution might have too many or too few
clusters. For more information, see Silhouette Value and Criterion.
Creation
Create a silhouette criterion clustering evaluation object by using the evalclusters function and specifying the criterion as
"silhouette".
You can then use compact to create a compact version of the
silhouette criterion clustering evaluation object. The function removes the contents of the
properties X, OptimalY, and
Missing.
Properties
Object Functions
Examples
More About
References
[1] Kaufman, L., and P. J. Rouseeuw. Finding Groups in Data: An Introduction to Cluster Analysis. Hoboken, NJ: John Wiley & Sons, Inc., 1990.
[2] Rouseeuw, P. J. “Silhouettes: a graphical aid to the interpretation and validation of cluster analysis.” Journal of Computational and Applied Mathematics. Vol. 20, No. 1, 1987, pp. 53–65.
Version History
Introduced in R2013b