lof
Syntax
Description
Use the lof function to create a local
outlier factor model for outlier detection and novelty detection.
Outlier detection (detecting anomalies in training data) — Use the output argument
tfoflofto identify anomalies in training data.Novelty detection (detecting anomalies in new data with uncontaminated training data) — Create a
LocalOutlierFactorobject by passing uncontaminated training data (data with no outliers) tolof. Detect anomalies in new data by passing the object and the new data to the object functionisanomaly.
LOFObj = lof(Tbl)LocalOutlierFactor
object for predictor data in the table Tbl.
LOFObj = lof(___,Name=Value)ContaminationFraction=0.1
Examples
Detect outliers (anomalies in training data) by using the lof function.
Load the sample data set NYCHousing2015.
load NYCHousing2015The data set includes 10 variables with information on the sales of properties in New York City in 2015. Display a summary of the data set.
summary(NYCHousing2015)
NYCHousing2015: 91446×10 table
Variables:
BOROUGH: double
NEIGHBORHOOD: cell array of character vectors
BUILDINGCLASSCATEGORY: cell array of character vectors
RESIDENTIALUNITS: double
COMMERCIALUNITS: double
LANDSQUAREFEET: double
GROSSSQUAREFEET: double
YEARBUILT: double
SALEPRICE: double
SALEDATE: datetime
Statistics for applicable variables:
NumMissing Min Median Max Mean Std
BOROUGH 0 1 3 5 2.8431 1.3343
NEIGHBORHOOD 0
BUILDINGCLASSCATEGORY 0
RESIDENTIALUNITS 0 0 1 8759 2.1789 32.2738
COMMERCIALUNITS 0 0 0 612 0.2201 3.2991
LANDSQUAREFEET 0 0 1700 29305534 2.8752e+03 1.0118e+05
GROSSSQUAREFEET 0 0 1056 8942176 4.6598e+03 4.3098e+04
YEARBUILT 0 0 1939 2016 1.7951e+03 526.9998
SALEPRICE 0 0 333333 4.1111e+09 1.2364e+06 2.0130e+07
SALEDATE 0 01-Jan-2015 09-Jul-2015 31-Dec-2015 07-Jul-2015 2470:47:17
Remove nonnumeric variables from NYCHousing2015. The data type of the BOROUGH variable is double, but it is a categorical variable indicating the borough in which the property is located. Remove the BOROUGH variable as well.
NYCHousing2015 = NYCHousing2015(:,vartype("numeric"));
NYCHousing2015.BOROUGH = [];Train a local outlier factor model for NYCHousing2015. Specify the fraction of anomalies in the training observations as 0.01.
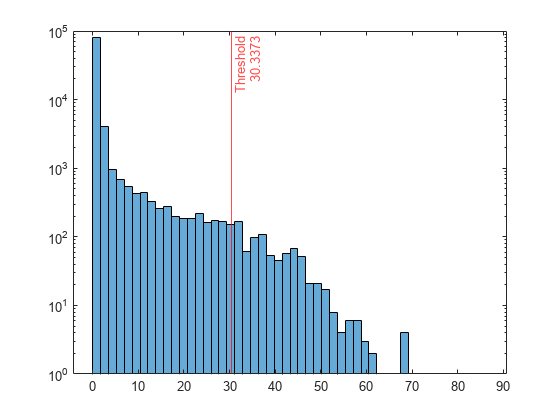
[Mdl,tf,scores] = lof(NYCHousing2015,ContaminationFraction=0.01);
Mdl is a LocalOutlierFactor object. lof also returns the anomaly indicators (tf) and anomaly scores (scores) for the training data NYCHousing2015.
Plot a histogram of the score values. Create a vertical line at the score threshold corresponding to the specified fraction.
h = histogram(scores,NumBins=50); h.Parent.YScale = 'log'; xline(Mdl.ScoreThreshold,"r-",["Threshold" Mdl.ScoreThreshold])
If you want to identify anomalies with a different contamination fraction (for example, 0.05), you can train a new local outlier factor model.
[newMdl,newtf,scores] = lof(NYCHousing2015,ContaminationFraction=0.05);
Note that changing the contamination fraction changes the anomaly indicators only, and does not affect the anomaly scores. Therefore, if you do not want to compute the anomaly scores again by using lof, you can obtain a new anomaly indicator with the existing score values.
Change the fraction of anomalies in the training data to 0.05.
newContaminationFraction = 0.05;
Find a new score threshold by using the quantile function.
newScoreThreshold = quantile(scores,1-newContaminationFraction)
newScoreThreshold = 6.7493
Obtain a new anomaly indicator.
newtf = scores > newScoreThreshold;
Create a LocalOutlierFactor object for uncontaminated training observations by using the lof function. Then detect novelties (anomalies in new data) by passing the object and the new data to the object function isanomaly.
Load the 1994 census data stored in census1994.mat. The data set consists of demographic data from the US Census Bureau to predict whether an individual makes over $50,000 per year.
load census1994census1994 contains the training data set adultdata and the test data set adulttest. The predictor data must be either all continuous or all categorical to train a LocalOutlierFactor object. Remove nonnumeric variables from adultdata and adulttest.
adultdata = adultdata(:,vartype("numeric")); adulttest = adulttest(:,vartype("numeric"));
Train a local outlier factor model for adultdata. Assume that adultdata does not contain outliers.
[Mdl,tf,s] = lof(adultdata);
Mdl is a LocalOutlierFactor object. lof also returns the anomaly indicators tf and anomaly scores s for the training data adultdata. If you do not specify the ContaminationFraction name-value argument as a value greater than 0, then lof treats all training observations as normal observations, meaning all the values in tf are logical 0 (false). The function sets the score threshold to the maximum score value. Display the threshold value.
Mdl.ScoreThreshold
ans = 28.6719
Find anomalies in adulttest by using the trained local outlier factor model.
[tf_test,s_test] = isanomaly(Mdl,adulttest);
The isanomaly function returns the anomaly indicators tf_test and scores s_test for adulttest. By default, isanomaly identifies observations with scores above the threshold (Mdl.ScoreThreshold) as anomalies.
Create histograms for the anomaly scores s and s_test. Create a vertical line at the threshold of the anomaly scores.
h1 = histogram(s,NumBins=50,Normalization="probability"); hold on h2 = histogram(s_test,h1.BinEdges,Normalization="probability"); xline(Mdl.ScoreThreshold,"r-",join(["Threshold" Mdl.ScoreThreshold])) h1.Parent.YScale = 'log'; h2.Parent.YScale = 'log'; legend("Training Data","Test Data",Location="north") hold off

Display the observation index of the anomalies in the test data.
find(tf_test)
ans = 0×1 empty double column vector
The anomaly score distribution of the test data is similar to that of the training data, so isanomaly does not detect any anomalies in the test data with the default threshold value. You can specify a different threshold value by using the ScoreThreshold name-value argument. For an example, see Specify Anomaly Score Threshold.
Input Arguments
Predictor data, specified as a table. Each row of Tbl
corresponds to one observation, and each column corresponds to one predictor variable.
Multicolumn variables and cell arrays other than cell arrays of character vectors are
not allowed.
The predictor data must be either all continuous or all categorical. If you specify
Tbl, the lof function assumes that a
variable is categorical if it is a logical vector, unordered categorical vector,
character array, string array, or cell array of character vectors. If
Tbl includes both continuous and categorical values, and you want
to identify all predictors in Tbl as categorical, you must specify
CategoricalPredictors as "all".
To use a subset of the variables in Tbl, specify the variables
by using the PredictorNames name-value argument.
Data Types: table
Predictor data, specified as a numeric matrix. Each row of X
corresponds to one observation, and each column corresponds to one predictor
variable.
The predictor data must be either all continuous or all categorical. If you specify
X, the lof function assumes that all
predictors are continuous. To identify all predictors in X as
categorical, specify CategoricalPredictors as
"all".
You can use the PredictorNames name-value argument to assign
names to the predictor variables in X.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: SearchMethod=exhaustive,Distance=minkowski uses the
exhaustive search algorithm with the Minkowski distance.
Maximum number of data points in the leaf node of the
Kd-tree, specified as a positive integer value. This argument is
valid only when SearchMethod is
"kdtree".
Example: BucketSize=40
Data Types: single | double
Size of the Gram matrix in megabytes, specified as a positive scalar or
"maximal". For the definition of the Gram matrix, see Algorithms. The
lof function can use a Gram matrix when the
Distance name-value argument is
"fasteuclidean".
When CacheSize is "maximal",
lof attempts to allocate enough memory for an entire
intermediate matrix whose size is MX-by-MX,
where MX is the number of rows of the input data,
X or Tbl. CacheSize
does not have to be large enough for an entire intermediate matrix, but must be at
least large enough to hold an MX-by-1 vector. Otherwise,
lof uses the "euclidean" distance.
If Distance is "fasteuclidean" and
CacheSize is too large or "maximal",
lof might attempt to allocate a Gram matrix that
exceeds the available memory. In this case, MATLAB® issues an error.
Example: CacheSize="maximal"
Data Types: double | char | string
Categorical predictor flag, specified as one of the following:
"all"— All predictors are categorical. By default,lofuses the Hamming distance ("hamming") for theDistancename-value argument.[]— No predictors are categorical, that is, all predictors are continuous (numeric). In this case, the defaultDistancevalue is"euclidean".
The predictor data for lof must be either all
continuous or all categorical.
If the predictor data is in a table (
Tbl),lofassumes that a variable is categorical if it is a logical vector, unordered categorical vector, character array, string array, or cell array of character vectors. IfTblincludes both continuous and categorical values, and you want to identify all predictors inTblas categorical, you must specifyCategoricalPredictorsas"all".If the predictor data is a matrix (
X),lofassumes that all predictors are continuous. To identify all predictors inXas categorical, specifyCategoricalPredictorsas"all".
lof encodes categorical variables as numeric variables by
assigning a positive integer value to each category. When you use categorical
predictors, ensure that you use an appropriate distance metric
(Distance).
Example: CategoricalPredictors="all"
Fraction of anomalies in the training data, specified as a numeric scalar in the
range [0,1].
If the
ContaminationFractionvalue is 0 (default), thenloftreats all training observations as normal observations, and sets the score threshold (ScoreThresholdproperty value ofLOFObj) to the maximum value ofscores.If the
ContaminationFractionvalue is in the range (0,1], thenlofdetermines the threshold value so that the function detects the specified fraction of training observations as anomalies.
Example: ContaminationFraction=0.1
Data Types: single | double
Covariance matrix, specified as a positive definite matrix of scalar values
representing the covariance matrix when the function computes the Mahalanobis
distance. This argument is valid only when Distance is
"mahalanobis".
The default value is the covariance matrix computed from the predictor data
(Tbl or X) after the function excludes
rows with duplicated values and missing values.
Data Types: single | double
Distance metric, specified as a character vector or string scalar.
If all the predictor variables are continuous (numeric) variables, then you can specify one of these distance metrics.
Value Description "euclidean"Euclidean distance
"fasteuclidean"Euclidean distance using an algorithm that usually saves time when the number of elements in a data point exceeds 10. See Algorithms.
"fasteuclidean"applies only to the"exhaustive"SearchMethod."mahalanobis"Mahalanobis distance — You can specify the covariance matrix for the Mahalanobis distance by using the
Covname-value argument."minkowski"Minkowski distance — You can specify the exponent of the Minkowski distance by using the
Exponentname-value argument."chebychev"Chebychev distance (maximum coordinate difference)
"cityblock"City block distance
"correlation"One minus the sample correlation between observations (treated as sequences of values)
"cosine"One minus the cosine of the included angle between observations (treated as vectors)
"spearman"One minus the sample Spearman's rank correlation between observations (treated as sequences of values)
Note
If you specify one of these distance metrics for categorical predictors, then the software treats each categorical predictor as a numeric variable for the distance computation, with each category represented by a positive integer. The
Distancevalue does not affect theCategoricalPredictorsproperty of the trained model.If all the predictor variables are categorical variables, then you can specify one of these distance metrics.
Value Description "hamming"Hamming distance, which is the percentage of coordinates that differ
"jaccard"One minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ
Note
If you specify one of these distance metrics for continuous (numeric) predictors, then the software treats each continuous predictor as a categorical variable for the distance computation. This option does not change the
CategoricalPredictorsvalue.
The default value is "euclidean" if all the predictor variables
are continuous, and "hamming" if all the predictor variables are
categorical.
If you want to use the Kd-tree algorithm
(SearchMethod="kdtree"Distance must be "euclidean",
"cityblock", "minkowski", or
"chebychev".
For more information on the various distance metrics, see Distance Metrics.
Example: Distance="jaccard"
Data Types: char | string
Minkowski distance exponent, specified as a positive scalar value. This argument
is valid only when Distance is
"minkowski".
Example: Exponent=3
Data Types: single | double
Tie inclusion flag indicating whether the software includes all the neighbors
whose distance values are equal to the kth smallest distance,
specified as logical 0 (false) or
1 (true). If IncludeTies
is true, the software includes all of these neighbors. Otherwise,
the software includes exactly k neighbors.
Example: IncludeTies=true
Data Types: logical
This property is read-only.
Predictor variable names, specified as a string array of unique names or cell array of
unique character vectors. The functionality of PredictorNames depends
on how you supply the predictor data.
If you supply
Tbl, then you can usePredictorNamesto specify which predictor variables to use. That is,lofuses only the predictor variables inPredictorNames.PredictorNamesmust be a subset ofTbl.Properties.VariableNames.By default,
PredictorNamescontains the names of all predictor variables inTbl.
If you supply
X, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the column order ofX. That is,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{"x1","x2",...}.
Data Types: string | cell
Nearest neighbor search method, specified as "kdtree" or
"exhaustive".
"kdtree"— This method uses the Kd-tree algorithm to find nearest neighbors. This option is valid when the distance metric (Distance) is one of the following:"euclidean"— Euclidean distance"cityblock"— City block distance"minkowski"— Minkowski distance"chebychev"— Chebychev distance
"exhaustive"— This method uses the exhaustive search algorithm to find nearest neighbors.When you compute local outlier factor values for the predictor data (
TblorX), theloffunction finds nearest neighbors by computing the distance values from all points in the predictor data to each point in the predictor data.When you compute local outlier factor values for new data
Xnewusing theisanomalyfunction, the function finds nearest neighbors by computing the distance values from all points in the predictor data (TblorX) to each point inXnew.
The default value is "kdtree" if the predictor data has 10 or
fewer columns, the data is not sparse, and the distance metric
(Distance) is valid for the Kd-tree
algorithm. Otherwise, the default value is "exhaustive".
Output Arguments
Trained local outlier factor model, returned as a LocalOutlierFactor object.
You can use the object function isanomaly
with LOFObj to find anomalies in new data.
Anomaly indicators, returned as a logical column vector. An element of
tf is logical 1 (true) when
the observation in the corresponding row of Tbl or
X is an anomaly, and logical 0
(false) otherwise. tf has the same length as
Tbl or X.
lof identifies observations with
scores above the threshold (ScoreThreshold property value of LOFObj) as
anomalies. The function determines the threshold value to detect the specified fraction
(ContaminationFraction name-value argument) of training
observations as anomalies.
Anomaly scores (local outlier factor values), returned as a
numeric column vector whose values are nonnegative. scores has the
same length as Tbl or X, and each element of
scores contains an anomaly score for the observation in the
corresponding row of Tbl or X. A score value
less than or close to 1 indicates a normal observation, and a value greater than 1 can
indicate an anomaly.
More About
The local outlier factor (LOF) algorithm detects anomalies based on the relative density of an observation with respect to the surrounding neighborhood.
The algorithm finds the k-nearest neighbors of an observation and computes the local reachability densities for the observation and its neighbors. The local outlier factor is the average density ratio of the observation to its neighbor. That is, the local outlier factor of observation p is
where
lrdk(·) is the local reachability density of an observation.
Nk(p) represents the k-nearest neighbors of observation p. You can specify the
IncludeTiesname-value argument astrueto include all the neighbors whose distance values are equal to the kth smallest distance, or specifyfalseto include exactly k neighbors. The defaultIncludeTiesvalue oflofisfalsefor more efficient performance. Note that the algorithm in [1] uses all the neighbors.|Nk(p)| is the number of observations in Nk(p).
For normal observations, the local outlier factor values are less than or close to 1,
indicating that the local reachability density of an observation is higher than or similar
to its neighbors. A local outlier factor value greater than 1 can indicate an anomaly. The
ContaminationFraction argument of lof and the ScoreThreshold
argument of isanomaly control the threshold for the local outlier
factor values.
The algorithm measures the density based on the reachability distance. The reachability distance of observation p with respect to observation o is defined as
where
dk(o) is the kth smallest distance among the distances from observation o to its neighbors.
d(p,o) is the distance between observation p and observation o.
The algorithm uses the reachability distance to reduce the statistical fluctuations of d(p,o) for the observations close to observation o.
The local reachability density of observation p is the reciprocal of the average reachability distance from observation p to its neighbors.
The density value can be infinity if the number of duplicates is greater than the number of
neighbors (k). Therefore, if the training data contains duplicates, the
lof and isanomaly functions use the weighted
local outlier factor (WLOF) algorithm. This algorithm computes the weighted local outlier
factors using the weighted local reachability density (wlrd).
where
and w(o) is the number of duplicates for observation o in the training data. After computing the weight values, the algorithm treats each set of duplicates as one observation.
A distance metric is a function that defines a distance between two observations. lof supports various distance metrics for continuous variables and categorical variables.
Given an mx-by-n data matrix X, which is treated as mx (1-by-n) row vectors x1, x2, ..., xmx, and an my-by-n data matrix Y, which is treated as my (1-by-n) row vectors y1, y2, ...,ymy, the various distances between the vector xs and yt are defined as follows:
Distance metrics for continuous (numeric) variables
Euclidean distance
The Euclidean distance is a special case of the Minkowski distance, where p = 2.
Fast Euclidean distance is the same as Euclidean distance, but uses an algorithm that usually saves time when the number of variables in an observation n exceeds 10. See Algorithms.
Mahalanobis distance
where C is the covariance matrix.
City block distance
The city block distance is a special case of the Minkowski distance, where p = 1.
Minkowski distance
For the special case of p = 1, the Minkowski distance gives the city block distance. For the special case of p = 2, the Minkowski distance gives the Euclidean distance. For the special case of p = ∞, the Minkowski distance gives the Chebychev distance.
Chebychev distance
The Chebychev distance is a special case of the Minkowski distance, where p = ∞.
Cosine distance
Correlation distance
where
and
Spearman distance is one minus the sample Spearman's rank correlation between observations (treated as sequences of values):
where
Distance metrics for categorical variables
Hamming distance
The Hamming distance is the percentage of coordinates that differ.
Jaccard distance is one minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ:
Algorithms
lof considers NaN, '' (empty character vector), "" (empty string), <missing>, and <undefined> values in Tbl and NaN values in X to be missing values.
lofdoes not use observations with missing values.lofassigns the anomaly score ofNaNand anomaly indicator offalse(logical 0) to observations with missing values.
The "fasteuclidean"
Distance calculates Euclidean distances using extra memory to save
computational time. This algorithm is named "Euclidean Distance Matrix Trick" in Albanie
[2] and elsewhere. Internal
testing shows that this algorithm saves time when the number of predictors exceeds 10. The
"fasteuclidean" distance does not support sparse data.
To find the matrix D of distances between all the points xi and xj, where each xi has n variables, the algorithm computes distance using the final line in the following equations:
The matrix in the last line of the equations is called the Gram matrix. Computing the set of squared distances is faster, but slightly less numerically stable, when you compute and use the Gram matrix instead of computing the squared distances by squaring and summing. For more information, see Albanie [2].
To store the Gram matrix, the software uses a cache with the default size of
1e3 megabytes. You can set the cache size using the
CacheSize name-value argument. If the value of
CacheSize is too large or "maximal",
lof might try to allocate a Gram matrix that exceeds the
available memory. In this case, MATLAB issues an error.
References
[1] Breunig, Markus M., et al. “LOF: Identifying Density-Based Local Outliers.” Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, 2000, pp. 93–104.
[2] Albanie, Samuel. Euclidean Distance Matrix Trick. June, 2019. Available at https://samuelalbanie.com/files/Euclidean_distance_trick.pdf.
Version History
Introduced in R2022bThe lof function supports the "fasteuclidean"
Distance algorithm. This algorithm usually computes distances faster
than the default "euclidean" algorithm when the number of variables in a
data point exceeds 10. The algorithm uses extra memory to store an intermediate Gram matrix
(see Algorithms). Set the size of this
memory allocation using the CacheSize name-value argument.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)