jacobiZeta
Jacobi zeta function
Syntax
Description
jacobiZeta(
returns the Jacobi Zeta Function of
u,m)u and m. If u or
m is an array, then jacobiZeta acts
element-wise.
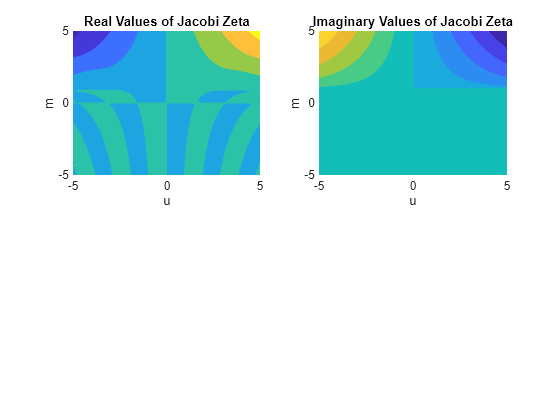
Examples
Input Arguments
More About
References
[1] Olver, F. W. J., A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, B. V. Saunders, H. S. Cohl, and M. A. McClain, eds., Chapter 22. Jacobian Elliptic Functions, NIST Digital Library of Mathematical Functions, Release 1.0.26 of 2020-03-15.
Version History
Introduced in R2017b