idwt
Single-level 1-D inverse discrete wavelet transform
Syntax
Description
x = idwt(cA,cD,wname)x based on the approximation and detail coefficients
cA and cD, respectively, using the
wavelet specified by wname. For more information, see
dwt.
Let la be the length of cA (which also
equals the length of cD), and lf the
length of the reconstruction filters associated with wname
(see wfilters). If the DWT
extension mode is set to periodization, then the length of
x is equal to 2la. Otherwise, the length of x is equal to 2la- 2lf+2. For more information, see dwtmode.
x = idwt(___,l)l central portion of the reconstruction.
This argument can be added to any of the previous input syntaxes
Examples
Input Arguments
Algorithms
Starting from the approximation and detail coefficients at level j, cAj and cDj, the inverse discrete wavelet transform reconstructs cAj−1, inverting the decomposition step by inserting zeros and convolving the results with the reconstruction filters.

where
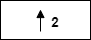 — Insert zeros at even-indexed elements
— Insert zeros at even-indexed elements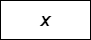 — Convolve with filter X
— Convolve with filter X — Take the central part of U with the
convenient length
— Take the central part of U with the
convenient length
References
[1] Daubechies, I. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1992.
[2] Mallat, S. G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 11, Issue 7, July 1989, pp. 674–693.
[3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.
Extended Capabilities
Version History
Introduced before R2006a