Main Content
Results for
Have you ever used Live Tasks in MATLAB? MathWorks development team would like to get some feedback on your experience – what did you like and not like. Especially, if you know about it but don’t use it frequently, we would like to understand why?
Please tell us what you think by submitting your response to this form https://forms.office.com/r/ui1EGqAFDx
how accurate are the answers of the AI Playground regarding information that are not specifiyed in the documentation?
A key aspect to masting MATLAB Graphics is getting a hang of the MATLAB Graphics Object Hierarchy which is essentially the structure of MATLAB figures that is used in the rendering pipeline. The base object is the Graphics Root (see groot) which contains the Figure. The Figure contains Axes or other containers such as a Tiled Chart Layout (see tiledlayout). Then these Axes can contain graphics primatives (the objects that contain data and get rendered) such as Lines or Patches.
Every graphics object has two important properties, the "Parent" and "Children" properties which can be used to access other objects in the tree. This can be very useful when trying to customize a pre-built chart (such as adding grid lines to both axes in an eye diagram chart) or when trying to access the axes of a non-current figure via a primative (so "gca" doesn't help out).
One last Tip and Trick with this is that you can declare graphics primatives without putting them on or creating an Axes by setting the first input argument to "gobjects(0)" which is an empty array of placeholder graphics objects. Then, when you have an Axes to plot the primitive on and are ready to render it, you can set the "Parent" of the object to your new Axes.
For Example:
l = line(gobjects(0), 1:10, 1:10);
...
...
...
l.Parent = gca;
Practicing navigating and exploring this tree will help propel your understanding of plotting in MATLAB.
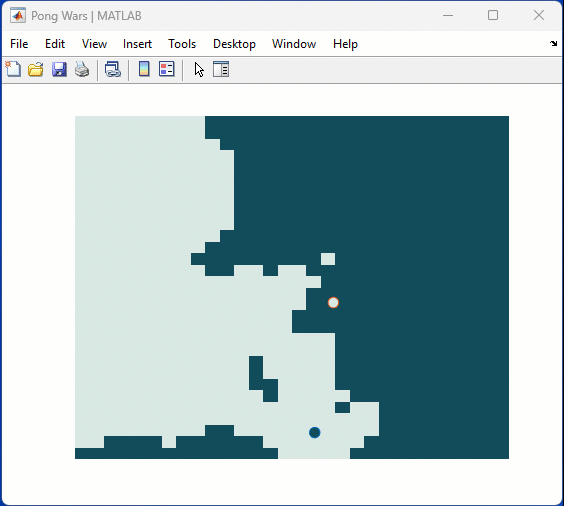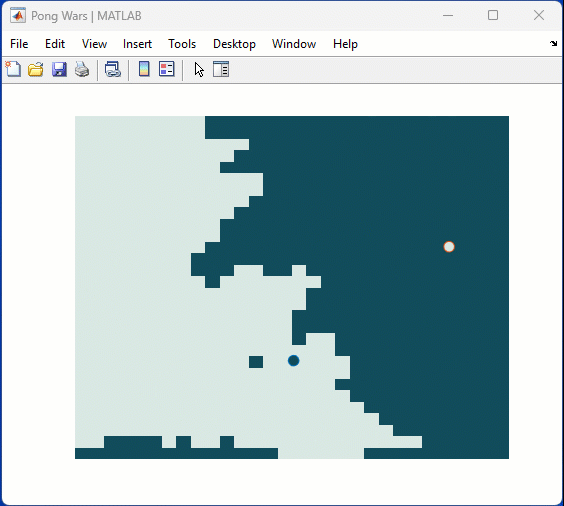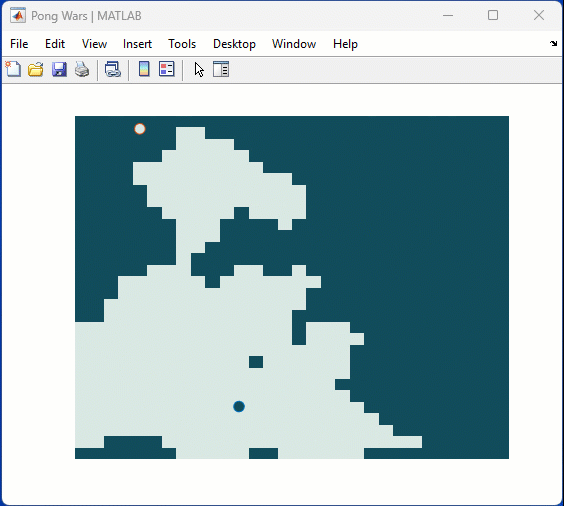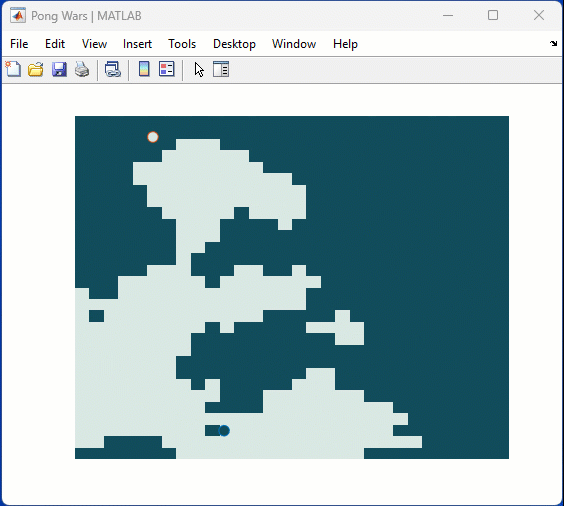
One of my colleauges, Michio, recently posted an implementation of Pong Wars in MATLAB
- Here's the code on GitHub.https://lnkd.in/gZG-AsFX
- If you want to open with MATLAB Online, click here https://lnkd.in/gahrTMW5
- He saw this first here: https://lnkd.in/gu_Z-Pks
Making me wonder about variations. What might the resulting patterns look with differing numbers of balls? Different physics etc?
We're thrilled to announce the roll-out of some new features that are going to supercharge your Playground experience! Here's what's new:
Copy/Download code from the script area
You can now effortlessly Copy/Download code from the script area with just a single click. Copy code or Download your script directly as .m files and keep your work organized and portable.We hope this will allow you to effortlessly transfer your work from Playground to MATLAB Desktop/Online.
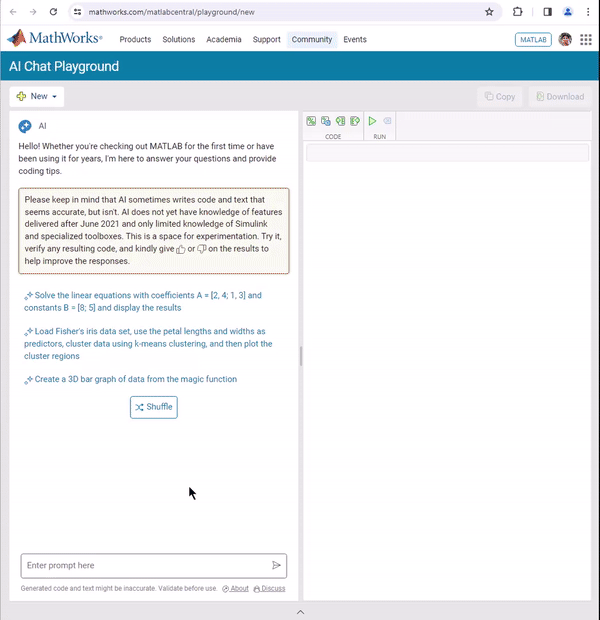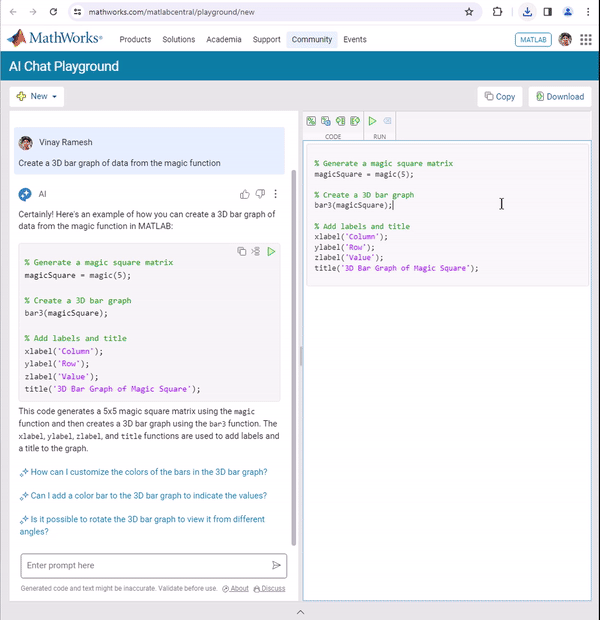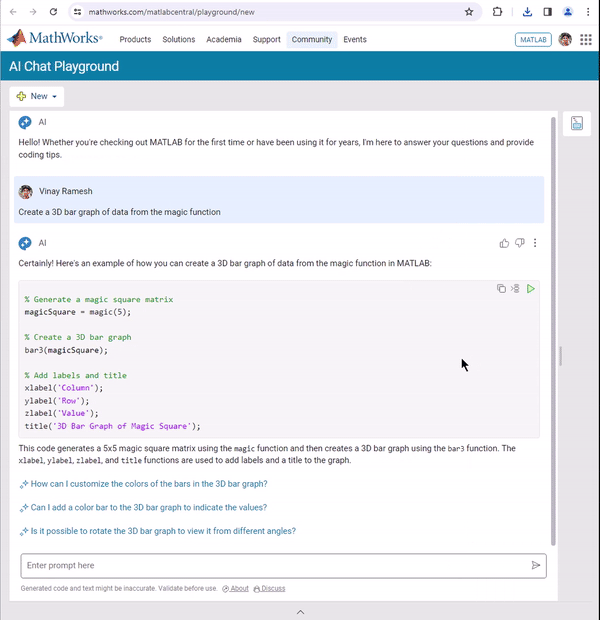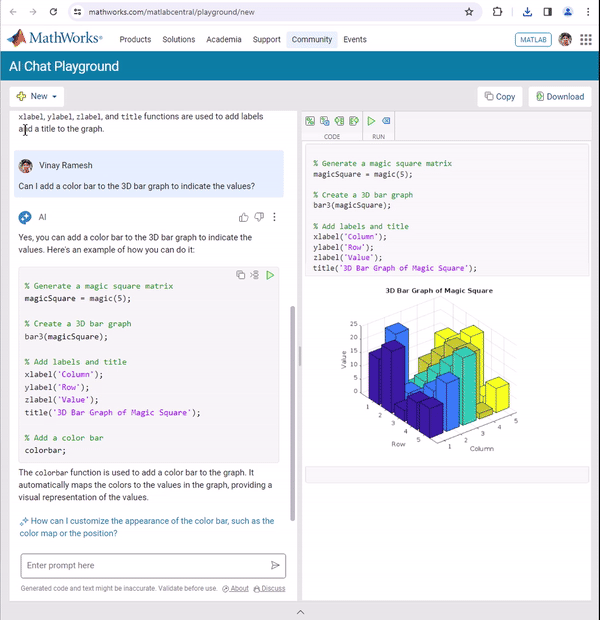
Run Code directly from the Chat panel
Execute code snippets from the chat section with a single click. This new affordance means saving a step since you no longer have to insert code and then hit run from the toolstrip to execute instead just hit run in the chat panel to see the output immediately in the script area
Enhanced visual Experience
Customize your Playground workspace by expanding or collapsing the chat and script sections. Focus on what matters most to you, whether it's AI chat or working on your script.
We hope you will love these updates. Try them out and let us know your feedback.
MathWorks just released three new courses on Coursera liseted below. If you work with image or video data and are wanting to incorporate deep learning techniques into your workflow, this is a great opporutnity. The course creators monitor the discussion forums, so you can ask questions and get feedback on your work. Below are links to the three courses and a quick description of a project you'll complete in each.
- Introduction to Computer Vision for Deep Learning. You'll train a classifier to classify images of people signing the American Sign Language alphabet.
- Deep Learning for Object Detection. Move from just classification to finding object locations. You'll train a model to find different types of parking available on the MathWorks campus.
- Advanced Deep Learning Techniques for Computer Vision. You'll train anomaly detection models for medical images and use AI-assisted labeling auto label images.
Can anyone provide insight into the intended difference between Discussions and Answers and what should be posted where?
Just scrolling through Discussions, I saw postst that seem more suitable Answers?
What exactly does Discussions bring to the table that wasn't already brought by Answers?
Maybe this question is more suitable for a Discussion ....
When I want to understand a problem, I'll often use different sources. I'll read different textbooks, blog posts, research papers and ask the same question to different people. The differences in the solutions are almost always illuminating.
I feel the same way about AIs. Sometimes, I don't want to ask *THE* AI...I want to ask a bunch of them. They'll have different strengths and weaknesses..different personalities if you want to think of it that way.
I've been playing with the AI chat arena and there really is a lot of difference between the answers returned by different models. https://lmarena.ai/?arena
I think it would be great if the MATLAB Chat playgroundwere to allow the user to change which AI they were talking with.
What does everyone else think?
how can i use this AI?
spy
Hello Community!
We are working on a new translation experience for the MathWorks website and products. The goal is to make it easy for people to see content in the best language for them.
Step 1 is learning from those of you who use another language instead of, or in addition to English. If this sounds like you, we'd love your response to a brief survey.
Feel free to comment here as well. Thanks in advance!
We've released an open-source implementation of STIPA (Speech Transmission Index for Public Address) on GitHub!
What is STIPA?
Speech Transmission Index is a metric designed to assess the quality of speech transmission through a communication channel. It quantifies the intelligibility of speech signals based on amplitude modulations, providing a standardized measure crucial for evaluating public address systems and communication equipment. STIPA is a version of STI using a simplified measurement method and only one test signal.
Quality Representation:
STI values range from 0 to 1, categorizing speech transmission quality from bad to excellent. The raw STI score can be transformed into the likelihood of intelligibility of syllables, words, and sentences being comprehended.
Verification Tests:
To ensure reliability, we've conducted verification tests according to the IEC 60286-16 standard. Download the test signals and run the stipaVerificationTests.m script from our GitHub repository.
Control Measurements:
We've performed comparative measurements in a university auditorium, showcasing the validity of our implementation.
License:
Our STIPA implementation is distributed under the GNU General Public License 3, reflecting our commitment to open-source collaboration.
I have been finding the AI Chat Playground very useful for daily MATLAB use. In particular it has been very useful for me in basically replacing or supplementing dives into MATLAB documentation. The documentation for MATLAB is in my experience uniformly excellent and thorough but it is sometimes lengthy and hard to parse and the AI Chat is a great one stop shop for many questions I have. However, I would find it very useful if the AI Chat could answer my queries and then also supply a link directly to the documentation. E.g. a box at the bottom of the answer that is basically
"Here is the documentation on the functions AI Chat referred to in this response"
could be neat.
Over at Reddit, a MATLAB user asked about when to use a script vs. a live script. How would you answer this?
Hi
I am using simulink for the frequency response analysis of the three phase induction motor stator winding.
The problem is that i can't optimise the pramaeter values manually, for this i have to use genetic algrothem. But iam stucked how to use genetic algorithum to optimise my circuit paramter values like RLC. Any guidence will be highly appreciated.
Starting with MATLAB can be daunting, but the right resources make all the difference. In my experience, the combination of MATLAB Onramp and Cody offers an engaging start.
MATLAB Onramp introduces you to MATLAB's basic features and workflows. Then practice your coding skill on Cody. Challenge yourself to solve 1 basic problem every day for a month! This consistent practice can significantly enhance your proficiency.
What other resources have helped you on your MATLAB journey? Share your recommendations and let's create a comprehensive learning path for beginners!
i am just thinking to make a project on software defined ratio SDR using matlab and its toolboxes but I am UG student in ECE don't know how to start can we have discussion here and want the guidance from the best or good persons in the field of wireless communication
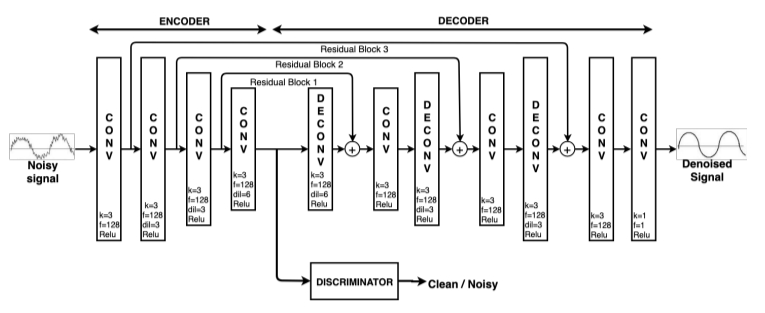
I am a beginner of deep learning, and meet with some problems in learning the MATLAB example "Denoise Signals with Adversarial Learning Denoiser Model", hope very much to get help!
1. visualizaition of the features
It is my understanding that the encoded representation of the autoencoder is the features of the original signal. However in this example, the output dimension of the encoder is 64xSignalLength. Does it mean that every sample point of the signal has 64 features?
2. usage of the residual blocks
The encoder-decoder model uses residual blocks (which contribute to reconstructing the denoised signal from the latent space, ). However, only the encoder output is connected to the discriminator. Doesn't it cause the prolem that most features will be learned by the residual blocks, and only a few features that could confuse the discriminator will be learned by the encoder and sent to the discriminator?
Hello everyone,
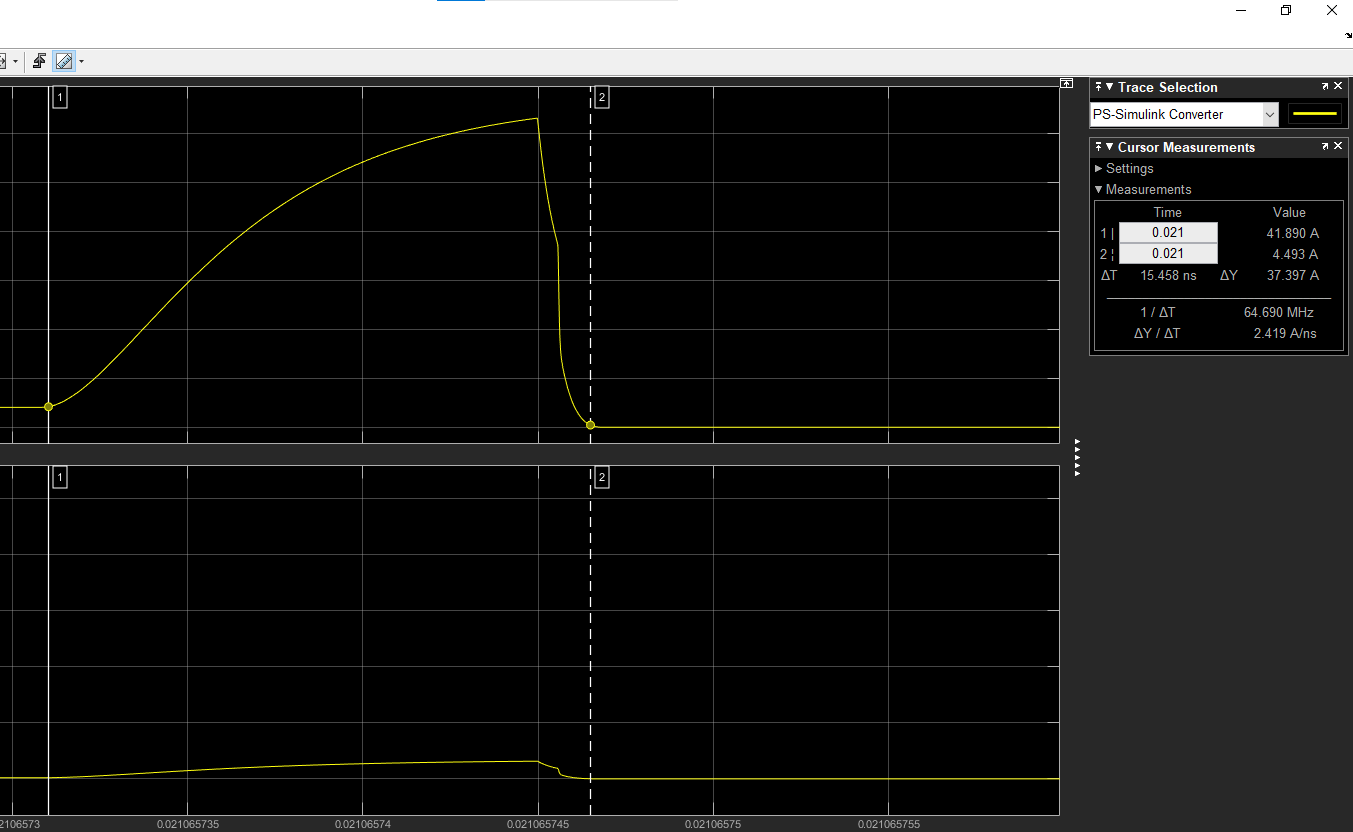
Im trying to simulate an 3-phase inverter, and for analysis of semicondcutor switches cuurent and voltage, I witness some unusal behaviour. I have connected a current sensor to the drain to calculate and visialize drain current, but the waveform is lookibg something like in picture if instaneous overshooting when going form high to low or vice versa, and the magnitude of the overshooting pulse can reach upto 500 Amps.
Kindly, guide me what am i doing here wrong? and one more thing is that I have set the Ids current to be 63Amps for N-channel Mosfet, but the output is 42-44 Amp max, what could be the reason behind it?
Thank you in advance!!