dsp.ColoredNoise

Generate colored noise signal

Description

The dsp.ColoredNoise System object™ generates a colored noise signal with a power spectral density (PSD) of 1/|f|^α over its entire frequency range. The inverse frequency power, α, can be any value in the interval [-2 2]. The type of colored noise the object generates depends on the Color you choose. When you set Color to 'custom', you can specify the power density of the noise through the InverseFrequencyPower property.

This object uses the default MATLAB^® random stream, RandStream. Reset the default stream for repeatable simulations.

To generate colored noise signal:

1. Create the dsp.ColoredNoise object and set its properties.

2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

cn = dsp.ColoredNoise

cn = dsp.ColoredNoise(Name=Value)

cn = dsp.ColoredNoise(pow,samp,numChan,Name=Value)

cn = dsp.ColoredNoise(color,samp,numChan,Name=Value)

Description

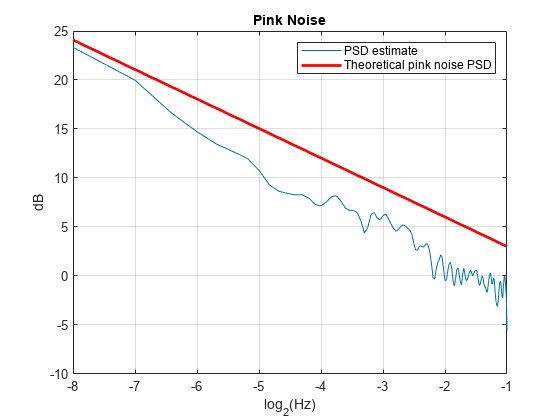
cn = dsp.ColoredNoise creates a colored noise object, cn, that outputs a noise signal one sample or frame at a time, with a 1/|f|^α spectral characteristic over its entire frequency range. Typical values for α are α = 1 (pink noise) and α = 2 (brownian noise).

cn = dsp.ColoredNoise(Name=Value) creates a colored noise object with each specified property set to the specified value. Enclose each property name in single quotes.

Example: dsp.ColoredNoise(Color='pink');

cn = dsp.ColoredNoise(pow,samp,numChan,Name=Value) creates a colored noise object with the InverseFrequencyPower property set to pow, the SamplesPerFrame property set to samp, and the NumChannels property set to numChan.

Example: dsp.ColoredNoise(1,44.1e3,1,OutputDataType='single');

cn = dsp.ColoredNoise(color,samp,numChan,Name=Value) creates a colored noise object with the Color property set to color, the SamplesPerFrame property set to samp, and the NumChannels property set to numChan.

Example: dsp.ColoredNoise('pink',1024,2,OutputDataType='single');

Properties

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Color — Noise color

'custom' (default) | 'pink' | 'white' | 'brown' | 'blue' | 'purple'

Noise color, specified as one of the following. Each color is associated with a specific inverse frequency power of the generated noise sequence.

• 'pink' –– The inverse frequency power α equals 1.

• 'white' –– α = 0.

• 'brown' –– α = 2. Also known as red or Brownian noise.

• 'blue' –– α = -1. Also known as azure noise.

• 'purple' –– α = -2. Also known as violet noise.

• 'custom' –– For noise with a custom inverse frequency power, α equals the value of the InverseFrequencyPower property.

  InverseFrequencyPower α can be any value in the interval [-2,2].

Data Types: char | string

InverseFrequencyPower — Inverse frequency power

1 (default) | real scalar in [-2 2]

Inverse frequency power α, specified as a real scalar in the interval [-2 2]. The inverse exponent defines the PSD of the random process as 1/|f|^α. Values of InverseFrequencyPower greater than 0 generate lowpass noise with a singularity (pole) at f = 0. These processes exhibit long memory. Values of InverseFrequencyPower less than 0 generate highpass noise with increments that are negatively correlated. These processes are referred to as anti-persistent. Special cases include:

• 1 –– Pink noise

• 2 –– Brown, red, or Brownian noise

• 0 –– White noise process with a flat PSD

• -1 –– Blue or azure noise

• -2 –– Purple of violet noise

In a log-log plot of power as a function of frequency, processes generated by this object exhibit an approximate linear relationship with slope equal to –α.

Dependencies

This property applies only when you set Color to 'custom'.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

SamplesPerFrameSource — Samples per frame source

'Property' (default) | 'Input port'

Source of the number of samples per frame, specified as 'Property' or 'Input port'.

Data Types: char | string

SamplesPerFrame — Number of samples per output channel

1024 (default) | positive integer

Number of samples per output channel, specified as a positive integer. This property determines the number of rows in the generated signal.

Dependencies

To enable this property, set SamplesPerFrameSource to 'Property'.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

MaxSamplesPerFrame — Maximum samples per frame

192000 (default) | positive integer

Maximum number of samples per frame, specified as a positive integer.

The value you specify in the MaxSamplesPerFrame property acts as an upper limit to the number of samples in each frame that the object generates. If you specify a value greater than MaxSamplesPerFrame, the number of samples in each frame that the object generates equals the value in the MaxSamplesPerFrame property.

Dependencies

To enable this property, set SamplesPerFrameSource to 'Input port'.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

NumChannels — Number of output channels

1 (default) | positive integer

Number of output channels, specified as an integer. This property determines the number of columns of the generated signal.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

RandomStream — Source of random number stream

'Global stream' (default) | 'mt19937ar with seed'

Source of the random number stream, specified as one of the following:

• 'Global stream' –– The current global random number stream is used for normally distributed random number generation.

• 'mt19937ar with seed' –– The mt19937ar algorithm is used for normally distributed random number generation. The reset function reinitializes the random number stream to the value of the Seed property.

Data Types: char | string

Seed — Initial seed

67 (default) | nonnegative integer

Initial seed of mt19937ar random number stream generator algorithm, specified as a nonnegative integer. The reset function reinitializes the random number stream to the value of the Seed property.

Dependencies

This property applies only when you set the RandomStream property to 'mt19937ar with seed'.

Data Types: double

BoundedOutput — Set output bounds to +1 and −1

false (default) | true

Specify the output to be bounded between +1 and −1, specified as:

• true –– The internal random source that generates the noise is uniform instead of Gaussian, and a gain is applied so that the absolute maximum output never exceeds 1.

  If Color is set to 'white', there is no color filter applied to the output of the random source. The output is uniform noise of amplitude between +1 and −1. The output distribution of filtered noise (such as pink noise) is quasi-Gaussian.

  If Color is set to any other option, then a coloring filter is applied to the output of the random source, followed by a gain which ensures that the absolute maximum output never exceeds 1.

• false –– The internal random source is Gaussian. The output is not bounded.

Data Types: logical

OutputDataType — Output data type

'double' (default) | 'single'

Output data type, specified as either 'double' or 'single'.

Data Types: char | string

Usage

Syntax

noiseOut = cn()

noiseOut = cn(L)

Description

noiseOut = cn() outputs one sample or one frame of colored noise data.

noiseOut = cn(L) outputs one frame of colored noise data of length L, where L is a nonnegative integer.

This syntax applies only when you set SamplesPerFrameSource to 'Input port'.

Output Arguments

noiseOut — Colored noise output

vector | matrix

Colored noise output, returned as a vector or a matrix. The SamplesPerFrame, NumChannels, and the OutputDataType properties specify the size and data type of the output.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

Common to All System Objects

step	Run System object algorithm
release	Release resources and allow changes to System object property values and input characteristics
reset	Reset internal states of System object

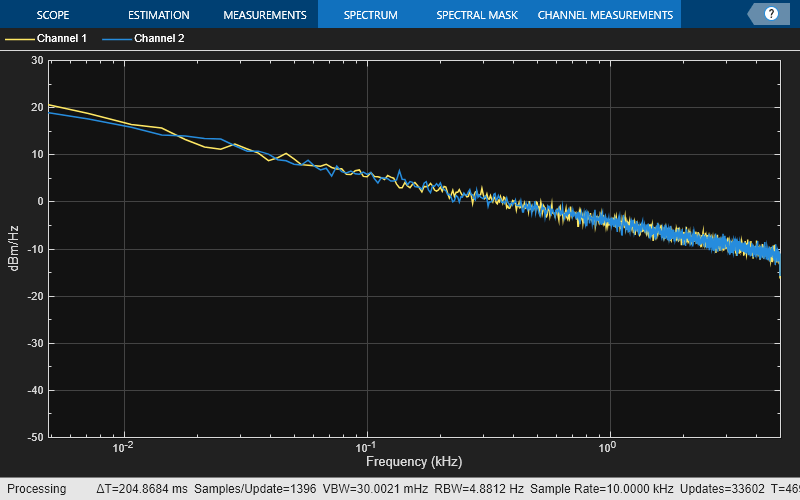
Examples

Measure Pink Noise Power in Octave Bands

The output from this example shows that pink noise has approximately equal power in octave bands.

Generate a single-channel signal of pink noise that is 44,100 samples in length. Set the random number generator to the default settings for reproducible results.

pinkNoise = dsp.ColoredNoise(1,44.1e3,1)

pinkNoise = 
  dsp.ColoredNoise with properties:

                    Color: 'custom'
    InverseFrequencyPower: 1
            BoundedOutput: false
              NumChannels: 1
    SamplesPerFrameSource: 'Property'
          SamplesPerFrame: 44100
           OutputDataType: 'double'
             RandomStream: 'Global stream'

rng default;
x = pinkNoise();

Set the sample rate to 44.1 kHz. Measure the power in octave bands beginning with 100-200 Hz and ending with 6.400-12.8 kHz. Display the results in a table.

beginfreq = 100;
endfreq = 200;
count = 1;
freqinterval = zeros(7,2);
Pwr = zeros(7,1);
while(endfreq<=44.1e3/2)
    freqinterval(count,:) = [beginfreq endfreq];
    Pwr(count) = bandpower(x,44.1e3,[beginfreq endfreq]);
    beginfreq = endfreq;
    endfreq = 2*endfreq;
    count = count+1;
end
Pwr = Pwr(:);
table(freqinterval,Pwr)

ans=7×2 table
    freqinterval       Pwr  
    _____________    _______

     100      200    0.17549
     200      400    0.20313
     400      800     0.2438
     800     1600     0.2503
    1600     3200    0.25233
    3200     6400    0.26828
    6400    12800    0.25211

The pink noise has roughly equal power in octave bands.

Rerun the preceding code with 'InverseFrequencyPower' equal to 0, which generates a white noise signal. A white noise signal has a flat power spectral density, or equal power per unit frequency. Set the random number generator to the default settings for reproducible results.

whiteNoise = dsp.ColoredNoise(0,44.1e3,1);
rng default;
x = whiteNoise();

Set the sample rate to 44.1 kHz. Measure the power in octave bands beginning with 100-200 Hz and ending with 6.400-12.8 kHz. Display the results in a table.

beginfreq = 100;
endfreq = 200;
count = 1;
while(endfreq<=44.1e3/2)
    freqinterval(count,:) = [beginfreq endfreq];
    Pwr(count) = bandpower(x,44.1e3,[beginfreq endfreq]);
    beginfreq = endfreq;
    endfreq = 2*endfreq;
    count = count+1;
end
Pwr = Pwr(:);
table(freqinterval,Pwr)

ans=7×2 table
    freqinterval        Pwr   
    _____________    _________

     100      200    0.0031417
     200      400    0.0073833
     400      800     0.017421
     800     1600     0.035926
    1600     3200     0.071139
    3200     6400      0.15183
    6400    12800      0.28611

White noise has approximately equal power per unit frequency, so octave bands have an unequal distribution of power. Because the width of an octave band increases with increasing frequency, the power per octave band increases for white noise.

PSD of Pink Noise Realization

Generate a pink noise signal 2048 samples in length. The sample rate is 1 Hz. Obtain an estimate of the power spectral density using Welch's overlapped segment averaging.

cn = dsp.ColoredNoise('pink',SamplesPerFrame=2048);
x = cn();
Fs = 1;
[Pxx,F] = pwelch(x,hamming(128),[],[],Fs,'psd');

Construct the theoretical PSD of the pink noise process.

PSDPink = 1./F(2:end);

Display the Welch PSD estimate of the noise along with the theoretical PSD on a log-log plot. Plot the frequency axis with a base-2 logarithmic scale to clearly show the octaves. Plot the PSD estimate in dB, $$10{\log }_{10}$$.

plot(log2(F(2:end)),10*log10(Pxx(2:end)))
hold on
plot(log2(F(2:end)),10*log10(PSDPink),'r',linewidth=2)
xlabel('log_2(Hz)')
ylabel('dB')
title('Pink Noise')
grid on
legend('PSD estimate','Theoretical pink noise PSD')
hold off

Two-Channel Brownian Noise

Generate two channels of Brownian noise by setting Color to 'brown' and NumChannels to 2. Specify the number of samples in each frame as an input while running the object algorithm.

cn = dsp.ColoredNoise('brown',SamplesPerFrameSource='Input port',...
    NumChannels=2)

cn = 
  dsp.ColoredNoise with properties:

                    Color: 'brown'
            BoundedOutput: false
              NumChannels: 2
    SamplesPerFrameSource: 'Input port'
       MaxSamplesPerFrame: 192000
           OutputDataType: 'double'
             RandomStream: 'Global stream'

x = cn(2048);
subplot(2,1,1)
plot(x(:,1)); title('Channel 1'); axis tight;
subplot(2,1,2)
plot(x(:,2)); title('Channel 2'); axis tight;

The sample rate is 1 Hz. Obtain Welch PSD estimates for both channels. The fourth argument of pwelch, NFFT, which is the number of FFT points, is empty. Hence, NFFT is set to 256. For even NFFT, The number of FFT points used to calculate the PSD estimate is (NFFT/2+1), which equals 129.

Fs = 1;
Pxx = zeros(129,size(x,2));
for nn = 1:size(x,2)
[Pxx(:,nn),F] = pwelch(x(:,nn),hamming(128),[],[],Fs,'psd');
end

Construct the theoretical PSD of a Brownian process. Plot the theoretical PSD along with both realizations on a log-log plot. Use a base-2 logarithmic scale for the frequency axis and plot the power spectral densities in dB.

PSDBrownian = 1./F(2:end).^2;
figure;
plot(log2(F(2:end)),10*log10(PSDBrownian),'k-.',linewidth=2);
hold on;
plot(log2(F(2:end)),10*log10(Pxx(2:end,:)));
xlabel('log_2(Hz)'); ylabel('dB');
grid on;
legend('Theoretical PSD','Channel 1', 'Channel 2');

Add Pink Noise at 0 dB SNR

Note: The audioDeviceWriter System object™ is not supported in MATLAB Online.

This example shows how to stream in an audio file and add pink noise at a 0 dB signal-to-noise ratio (SNR). The example reads in frames of an audio file 1024 samples in length, measures the root mean square (RMS) value of the audio frame, and adds pink noise with the same RMS value as the audio frame.

Set up the System objects. Set 'SamplesPerFrame' for both the file reader and the colored noise generator to 1024 samples. Set Color to 'pink' to generate pink noise with a $$1/|f|$$ power spectral density.

N = 1024;
afr = dsp.AudioFileReader(Filename='speech_dft.mp3',...
    SamplesPerFrame=N);
adw = audioDeviceWriter(SampleRate=afr.SampleRate);
cn = dsp.ColoredNoise('pink',SamplesPerFrame=N);

Stream the audio file in 1024 samples at a time. Measure the signal RMS value for each frame, generate a frame of pink noise equal in length, and scale the RMS value of the pink noise to match the signal. Add the scaled noise to the signal and play the output.

while ~isDone(afr)
    audio = afr();
    speechRMS = rms(audio);
    noise = cn();
    noiseRMS = rms(noise);
    noise = noise*(speechRMS/noiseRMS);
    sigPlusNoise = audio+noise;
    adw(sigPlusNoise);   
end
release(afr);            
release(adw);

Averaged Power Spectrum of Pink Noise

Generate two-channels of pink noise and compute the power density spectrum.

Set up the colored noise generator to generate two channels of pink noise with 1024 samples. Set up the spectrum analyzer to compute modified periodograms using a Hamming window and 50% overlap.

pinkNoise = dsp.ColoredNoise('pink',1024,2);
sa = spectrumAnalyzer(SpectrumType='power-density',...
    Method='welch',...
    AveragingMethod='exponential',...
    ForgettingFactor=0.95,...
    OverlapPercent=50,Window='hamming',...
    PlotAsTwoSidedSpectrum=false, ...
    FrequencyScale='log',YLimits=[-50 30]);

Run the simulation for 30 seconds.

tic
while toc < 30
    pink = pinkNoise();      
    sa(pink);
end

More About

Colored Noise Processes

Many phenomena in diverse fields, such as hydrology and finance, produce time series with PSD functions that follow a power law of the form

$$S(f)=\frac{L(f)}{|f{|}^{\alpha }}$$

where α is a real number in the interval [-2,2] and $$L(f)$$ is a positive, slowly-varying or constant function. Plotting the PSD of such processes on a log-log plot displays an approximate linear relationship between the log frequency and log PSD with slope equal to -α

$$\ln S(f)=-\alpha \ln \left|f\right|+\ln L(f).$$

It is often convenient to plot the PSD in dB as a function of the frequency on a base-2 logarithmic scale. The slope of the plot is then dB/octave. Rewriting the preceding equation, you obtain

$$10\log S(f)=-10\alpha \frac{\ln (2){\log }_2(f)}{\ln (10)}+10\frac{\ln (L(f))}{\ln (10)}$$

with the slope in dB/octave given by

$$-10\alpha \frac{\ln (2){\log }_2(f)}{\ln (10)}$$

If α > 0, S(f) goes to infinity as the frequency, f, approaches 0. Stochastic processes with PSDs of this form exhibit long memory. Long-memory processes have autocorrelations that persist for a long time as opposed to decaying exponentially like many common time-series models. If α<0, the process is antipersistent and exhibits negative correlation between increments [1].

Special examples of $$\frac{1}{|f{|}^{\alpha }}$$ processes include:

• α = 0 — White noise, where L(f) is a constant proportional to the process variance.

• α = 1 — Pink, or flicker noise. Pink noise has equal energy per octave. See Measure Pink Noise Power in Octave Bands for a demonstration. The power spectral density of pink noise decreases 3 dB per octave.

• α = 2 — brown noise, or Brownian motion. Brownian motion is a nonstationary process with stationary increments. You can think of Brownian motion as the integral of a white noise process. Even though Brownian motion is nonstationary, you can still define a generalized power spectrum, which behaves like $$\frac{1}{|f{|}^2}$$. Accordingly, power in a brown noise decreases 6 dB per octave.

• α = −1 — blue noise. The power spectral density of blue noise increases 3 dB per octave.

• α = −2 — violet, or purple noise. The power spectral density of violet noise increases 6 dB per octave. You can think of violet noise as the derivative of white noise process.

Algorithms

The figure shows the overall process of generating the colored noise.

The random stream generator produces a stream of white noise that is either Gaussian or uniform in distribution. A coloring filter applied to the white noise generates colored noise with a power spectral density (PSD) function given by:

$$S(f)=\frac{L(f)}{|f{|}^{\alpha }}$$

When α, the inverse frequency power, equals 0, no coloring filter is applied to the output of the random stream generator. If the bounded option is enabled, the output is uniform white noise with amplitude between +1 and −1. If the bounded output is not enabled, the output is a Gaussian white noise and the values are not bounded between +1 and −1. If α is set to any other value, then a coloring filter is applied to the output of the random stream generator. If the bounded output option is enabled, a gain g is applied to the output of the coloring filter to ensure that the absolute maximum output never exceeds 1.

For details on colored noise processes and how the value of α affects the PSD of the colored noise, see Colored Noise Processes.

When the inverse frequency power α is positive, the colored noise is generated using an auto regressive (AR) model of order 63. The AR coefficients are:

$$\begin{array}{l}{a}_0=1,\\ a_k=(k-1-\frac{\alpha }{2})\frac{a_{k-1}}{k},k=1,2,\dots ,63\end{array}$$

Pink and brown noises are special cases, which are generated from specially tuned SOS filters of orders 12 and 10, respectively. These filters are optimized for better performance.

When the inverse frequency power α is negative, the colored noise is generated using a moving average (MA) model of order 255. The MA coefficients are:

$$\begin{array}{l}{b}_0=1,\\ b_k=\left(k-1+\frac{\alpha }{2}\right)\frac{b_{k-1}}{k},k=1,2,\cdots ,255\end{array}$$

Purple noise is generated from a first order filter, B = [1 −1].

The coloring filters applied (except pink, brown, and purple) are detailed on pp. 820–822 in [2].

References

[1] Beran, J., Y. Feng, S. Ghosh, and R. Kulik, Long-Memory Processes: Probabilistic Properties and Statistical Methods. NewYork: Springer, 2013.

[2] Kasdin, N.J. "Discrete Simulation of Colored Noise and Stochastic Processes and 1/f^α Power Law Noise Generation." Proceedings of the IEEE^®, Vol. 83, No. 5, 1995, pp. 802–827.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

See System Objects in MATLAB Code Generation (MATLAB Coder).

Version History

Introduced in R2014a

R2022b: Variable-sized output frames in dsp.ColoredNoise object

Starting in R2022b, dsp.ColoredNoise object can generate colored noise signals of variable-sized output frames.

You can specify the frame size of the output colored noise signal as a nonnegative scalar value that is less than or equal to the MaxSamplesPerFrame property.