filter
Filter disturbances through vector autoregression (VAR) model
Syntax
Description
Y = filter(Mdl,Z)Y containing the multivariate
response series, which results from filtering the underlying input numeric array
Z containing the multivariate disturbance series. The
series in Z are associated with the model innovations
process through the fully specified VAR(p) model
Mdl.
Tbl2 = filter(Mdl,Tbl1,Presample=Presample)Tbl2 containing the multivariate response series, which results from filtering the underlying multivariate disturbance series in the input table or timetable Tbl1. filter initializes the response series using the required table or timetable of presample data in Presample. Variables in Tbl1 are associated with the model innovations process through Mdl. (since R2022b)
filter selects the variables in Mdl.SeriesNames or all variables in Tbl1. To select different disturbance variables in Tbl1 to filter through the model, use the DisturbanceVariables name-value argument. filter selects the same variables for Presample by default, but you can select different variables by using the PresampleResponseVariables name-value argument.
[___] = filter(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name=Value)filter returns the output argument combination for the
corresponding input arguments. For example, filter(Mdl,Z,Y0=PS,X=Exo) filters
the numeric array of disturbances Z through the
VAR(p) model Mdl, and specifies the
numeric array of presample response data PS and the numeric
matrix of exogenous predictor data Exo for the model
regression component.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
filtercomputes filtered responsesYand innovationsEusing this process for each pagejinZ.If
Scaleistrue, thenE(:,:,=j)L*Z(:,:,, wherej)L=chol(Mdl.Covariance,'lower'). Otherwise,E(:,:,=j)Z(:,:,. Set et =j)E(:,:,.j)Y(:,:,is yt in this system of equations.j)For variable definitions, see More About.
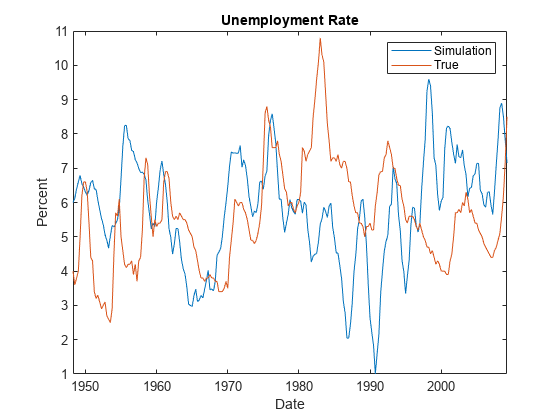
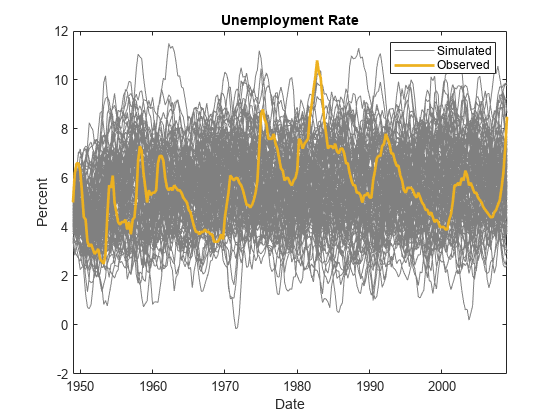
filtergeneralizessimulate. Both functions filter a disturbance series through a model to produce responses and innovations. However, whereassimulategenerates a series of mean-zero, unit-variance, independent Gaussian disturbancesZto form innovationsE=L*Z,filterenables you to supply disturbances from any distribution.filteruses this process to determine the time origin t0 of models that include linear time trends:If you specify
Zand you do not specify a presample by using theY0name-value argument, t0 = 0.Otherwise, if you specify
Tbl1or you supply a presample,filtersets t0 tosize(–Y0,1)Mdl.P, whereY0Y0orPresample. Therefore, the times in the trend component are t = t0 + 1, t0 + 2,..., t0 +numobs, wherenumobsis the effective sample size (size(Z,1), afterfilterremoves missing values, orheight(Tbl1)). This convention is consistent with the default behavior of model estimation, in whichestimateremoves the firstMdl.Presponses, reducing the effective sample size. Althoughfilterexplicitly uses the firstMdl.Ppresample responses inY0Y0Z, excluding missing values, orTbl1) determines t0.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.
[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.
[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin: Springer, 2005.