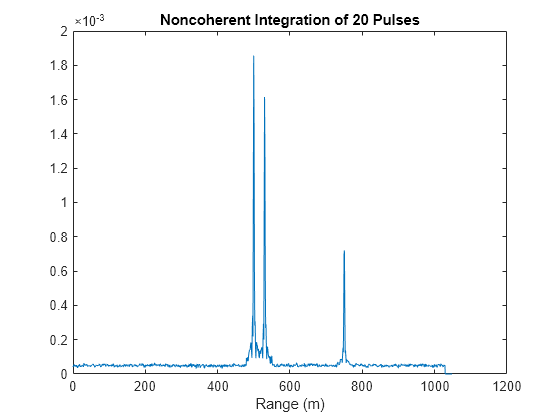
phased.RangeResponse

Range response

Description

The phased.RangeResponse System object™ performs range filtering on fast-time (range) data, using either a matched filter or an FFT-based algorithm. The output is typically used as input to a detector. Matched filtering improves the SNR of pulsed waveforms. For continuous FM signals, FFT processing extracts the beat frequency of FMCW waveforms. Beat frequency is directly related to range.

The input to the range response object is a radar data cube. The organization of the data cube follows the Phased Array System Toolbox™ convention.

• The first dimension of the cube represents the fast-time samples or ranges of the received signals.

• The second dimension represents multiple spatial channels, such as different sensors or beams.

• The third dimension, slow-time, represent pulses.

Range filtering operates along the fast-time dimension of the cube. Processing along the other dimensions is not performed. If the data contains only one channel or pulse, the data cube can contain fewer than three dimensions. Because this object performs no Doppler processing, you can use the object to process noncoherent radar pulses.

The output of the range response object is also a data cube with the same number of dimensions as the input. Its first dimension contains range-processed data but its length can differ from the first dimension of the input data cube.

To compute the range response:

1. Define and set up your phased.RangeResponse System object. See Construction.

2. Call the step method to compute the range response using the properties you specify for the phased.RangeResponse System object.

Note

Instead of using the step method to perform the operation defined by the System object, you can call the object with arguments, as if it were a function. For example, y = step(obj,x) and y = obj(x) perform equivalent operations.

Construction

response = phased.RangeResponse creates a range response System object, response.

response = phased.RangeResponse(Name,Value) creates a System object, response, with each specified property Name set to the specified Value. You can specify additional name and value pair arguments in any order as (Name1,Value1,...,NameN,ValueN).

Properties

RangeMethod — Range processing method

'Matched filter' (default) | 'FFT'

Range processing method, specified as 'Matched filter' or 'FFT'.

• 'Matched filter' — The object match-filters the incoming signal. This approach is commonly used for pulsed signals, where the matched filter is the time reverse of the transmitted signal.

• 'FFT' — The object applies an FFT to the input signal. This approach is commonly used for chirped signals such as FMCW and linear FM pulsed signals.

Example: 'Matched filter'

Data Types: char

PropagationSpeed — Signal propagation speed

physconst('LightSpeed') (default) | real-valued positive scalar

Signal propagation speed, specified as a real-valued positive scalar. Units are in meters per second. The default propagation speed is the value returned by physconst('LightSpeed').

Example: 3e8

Data Types: single | double

SampleRate — Signal sample rate

1e6 (default) | positive real-valued scalar

Signal sample rate, specified as a positive real-valued scalar. Units are in hertz.

Example: 1e6

Data Types: single | double

SweepSlope — Linear FM sweep slope

1.0e9 (default) | scalar

Linear FM sweep slope, specified as a scalar. The fast-time dimension of the signal input argument to step must correspond to sweeps having this slope.

Example: 1.5e9

Dependencies

To enable this property, set the RangeMethod property to 'FFT'.

Data Types: single | double

DechirpInput — Enable dechirping of input signals

false (default) | true

Option to enable dechirping of input signals, specified as false or true. Set this property to false to indicate that the input signal is already dechirped and no dechirp operation is necessary. Set this property to true when the input signal requires dechirping.

Dependencies

To enable this property, set the RangeMethod property to 'FFT'.

Data Types: logical

DecimationFactor — Decimation factor for dechirped signals

1 (default) | positive integer

Decimation factor for dechirped signals, specified as a positive integer. The decimation algorithm uses a 30th-order FIR filter generated by fir1(30,1/D), where D is the decimation factor. The default value of 1 implies no decimation.

When processing FMCW signals, decimating the dechirped signal is useful for reducing the load on A/D converters.

Dependencies

To enable this property, set the RangeMethod property to 'FFT' and the DechirpInput property to true.

Data Types: single | double

RangeFFTLengthSource — Source of FFT length for range processing of dechirped signals

'Auto (default) | 'Property'

Source of the FFT length used for the range processing of dechirped signals, specified as 'Auto' or 'Property'.

• 'Auto' — The FFT length equals the length of the fast-time dimension of the input data cube.

• 'Property' — Specify the FFT length by using the RangeFFTLength property.

Dependencies

To enable this property, set the RangeMethod property to 'FFT'.

Data Types: char

RangeFFTLength — FFT length used for range processing

1024 (default) | positive integer

FFT length used for range processing, specified as a positive integer.

Dependencies

To enable this property, set the RangeMethod property to 'FFT' and the RangeFFTLengthSource property to 'Property'

Data Types: single | double

RangeWindow — FFT weighting window for range processing

'None' (default) | 'Hamming' | 'Chebyshev' | 'Hann' | 'Kaiser' | 'Taylor' | 'Custom'

FFT weighting window for range processing, specified as 'None', 'Hamming', 'Chebyshev', 'Hann', 'Kaiser', 'Taylor', or 'Custom'.

If you set this property to 'Taylor', the generated Taylor window has four nearly constant sidelobes next to the mainlobe.

Dependencies

To enable this property, set the RangeMethod property to 'FFT'.

Data Types: char

RangeSidelobeAttenuation — Sidelobe attenuation for range processing

30 (default) | positive scalar

Sidelobe attenuation for range processing, specified as a positive scalar. Attenuation applies to Kaiser, Chebyshev, or Taylor windows. Units are in dB.

Dependencies

To enable this property, set the RangeMethod property to 'FFT' and the RangeWindow property to 'Kaiser', 'Chebyshev', or 'Taylor'.

Data Types: single | double

CustomRangeWindow — Custom window for range processing

@hamming (default) | function handle | cell array

Custom window for range processing, specified as a function handle or a cell array containing a function handle as its first entry. If you do not specify a window length, the object computes the window length and passes that into the function. If you specify a cell array, the remaining cells of the array can contain arguments to the function. If you use only the function handle without passing in arguments, all arguments take their default values.

If you write your own window function, the first argument must be the length of the window.

Note

Instead of using a cell array, you can pass in all arguments by constructing a handle to an anonymous function. For example, you can set the value of CustomRangeWindow to @(n)taylorwin(n,nbar,sll), where you have previously set the values of nbar and sll.

Example: {@taylor,5,-35}

Dependencies

To enable this property, set the RangeMethod property to 'FFT' and the RangeWindow property to 'Custom'.

Data Types: function_handle | cell

ReferenceRangeCentered — Set reference range at center of range grid

true (default) | false

Set reference range at center of range grid, specified as true or false. Setting this property to true enables you to set the reference range at the center of the range grid. Setting this property to false sets the reference range to the beginning of the range grid.

Dependencies

To enable this property, set the RangeMethod to 'FFT'.

Data Types: logical

ReferenceRange — Reference range of range grid

0.0 (default) | nonnegative scalar

Reference range of the range grid, specified as a nonnegative scalar.

• If you set the RangeMethod property to 'Matched filter', the reference range is set to the start of the range grid.

• If you set the RangeMethod property to 'FFT', the reference range is determined by the ReferenceRangeCentered property.

  • When you set the ReferenceRangeCentered property to true, the reference range is set to the center of the range grid.

  • When you set the ReferenceRangeCentered property to false, the reference range is set to the start of the range grid.

  Units are in meters.

This property is tunable.

Example: 1000.0

Data Types: single | double

MaximumNumInputSamplesSource — Source of maximum number of samples

'Auto' (default) | 'Property'

The source of the maximum number of samples the input signal, specified as 'Auto' or 'Property'. When you set this property to 'Auto', the object automatically allocates enough memory to buffer the first input signal. When you set this property to 'Property', you specify the maximum number of samples in the input signal using the MaximumNumInputSamples property. Any input signal longer than that value is truncated.

To use this object with variable-size input signals in a MATLAB^® Function Block in Simulink^®, set the MaximumNumInputSamplesSource property to 'Property' and set a value for the MaximumNumInputSamples property.

Example: 'Property'

MaximumNumInputSamples — Maximum number of input signal samples

100 (default) | positive integer

Maximum number of samples in the input signal, specified as a positive integer. Any input signal longer than this value is truncated. The input signal is the first argument to the step method. The number of samples is the number of rows in the input.

Example: 2048

Dependencies

To enable this property, set the RangeMethod property to 'Matched filter' and set the MaximumNumInputSamplesSource property to 'Property'.

Data Types: single | double

Methods

plotResponse	Plot range response
step	Range response

Common to All System Objects
release	Allow System object property value changes

Examples

Range Response of Three Targets

Compute the radar range response of three targets by using the phased.RangeResponse System object™. The transmitter and receiver are collocated isotropic antenna elements forming a monostatic radar system. The transmitted signal is a linear FM waveform with a pulse repetition interval of 7.0 μs and a duty cycle of 2%. The operating frequency is 77 GHz and the sample rate is 150 MHz.

fs = 150e6;
c = physconst('LightSpeed');
fc = 77e9;
pri = 7e-6;
prf = 1/pri;

Set up the scenario parameters. The radar transmitter and receiver are stationary and located at the origin. The targets are 500, 530, and 750 meters from the radars on the x-axis. The targets move along the x-axis at speeds of −60, 20, and 40 m/s. All three targets have a nonfluctuating radar cross-section (RCS) of 10 dB.

Create the target and radar platforms.

Numtgts = 3;
tgtpos = zeros(Numtgts);
tgtpos(1,:) = [500 530 750];
tgtvel = zeros(3,Numtgts);
tgtvel(1,:) = [-60 20 40];
tgtrcs = db2pow(10)*[1 1 1];
tgtmotion = phased.Platform(tgtpos,tgtvel);
target = phased.RadarTarget('PropagationSpeed',c,'OperatingFrequency',fc, ...
    'MeanRCS',tgtrcs);
radarpos = [0;0;0];
radarvel = [0;0;0];
radarmotion = phased.Platform(radarpos,radarvel);

Create the transmitter and receiver antennas.

txantenna = phased.IsotropicAntennaElement;
rxantenna = clone(txantenna);

Set up the transmitter-end signal processing. Create an upsweep linear FM signal with a bandwidth of half the sample rate. Find the length of the pri in samples and then estimate the rms bandwidth and range resolution.

bw = fs/2;
waveform = phased.LinearFMWaveform('SampleRate',fs, ...
    'PRF',prf,'OutputFormat','Pulses','NumPulses',1,'SweepBandwidth',fs/2, ...
    'DurationSpecification','Duty cycle','DutyCycle',0.02);
sig = waveform();
Nr = length(sig);
bwrms = bandwidth(waveform)/sqrt(12);
rngrms = c/bwrms;

Set up the transmitter and radiator System object properties. The peak output power is 10 W and the transmitter gain is 36 dB.

peakpower = 10;
txgain = 36.0;
transmitter = phased.Transmitter( ...
    'PeakPower',peakpower, ...
    'Gain',txgain, ...
    'InUseOutputPort',true);
radiator = phased.Radiator( ...
    'Sensor',txantenna, ...
    'PropagationSpeed',c, ...
    'OperatingFrequency',fc);

Create a free-space propagation channel in two-way propagation mode.

channel = phased.FreeSpace( ...
    'SampleRate',fs, ...    
    'PropagationSpeed',c, ...
    'OperatingFrequency',fc, ...
    'TwoWayPropagation',true);

Set up the receiver-end processing. The receiver gain is 42 dB and noise figure is 10.

collector = phased.Collector( ...
    'Sensor',rxantenna, ...
    'PropagationSpeed',c, ...
    'OperatingFrequency',fc);
rxgain = 42.0;
noisefig = 10;
receiver = phased.ReceiverPreamp( ...
    'SampleRate',fs, ...
    'Gain',rxgain, ...
    'NoiseFigure',noisefig);

Loop over 128 pulses to build a data cube. For each step of the loop, move the target and propagate the signal. Then put the received signal into the data cube. The data cube contains the received signal per pulse. Ordinarily, a data cube has three dimensions, where last dimension corresponds to antennas or beams. Because only one sensor is used in this example, the cube has only two dimensions.

The processing steps are:

1. Move the radar and targets.

2. Transmit a waveform.

3. Propagate the waveform signal to the target.

4. Reflect the signal from the target.

5. Propagate the waveform back to the radar. Two-way propagation mode enables you to combine the returned propagation with the outbound propagation.

6. Receive the signal at the radar.

7. Load the signal into the data cube.

Np = 128;
cube = zeros(Nr,Np);
for n = 1:Np
    [sensorpos,sensorvel] = radarmotion(pri);
    [tgtpos,tgtvel] = tgtmotion(pri);
    [tgtrng,tgtang] = rangeangle(tgtpos,sensorpos);
    sig = waveform();
    [txsig,txstatus] = transmitter(sig);
    txsig = radiator(txsig,tgtang);
    txsig = channel(txsig,sensorpos,tgtpos,sensorvel,tgtvel);    
    tgtsig = target(txsig);   
    rxcol = collector(tgtsig,tgtang);
    rxsig = receiver(rxcol);
    cube(:,n) = rxsig;
end

Display the image of the data cube containing signals per pulse.

imagesc([0:(Np-1)]*pri*1e6,[0:(Nr-1)]/fs*1e6,abs(cube))
xlabel('Slow Time {\mu}s')
ylabel('Fast Time {\mu}s')

Create a phased.RangeResponse System object in matched filter mode. Then, display the range response image for the 128 pulses. The image shows range vertically and pulse number horizontally.

matchingcoeff = getMatchedFilter(waveform);
ndop = 128;
rangeresp = phased.RangeResponse('SampleRate',fs,'PropagationSpeed',c);
[resp,rnggrid] = rangeresp(cube,matchingcoeff);
imagesc([1:Np],rnggrid,abs(resp))
xlabel('Pulse')
ylabel('Range (m)')

Integrate 20 pulses noncoherently.

intpulse = pulsint(resp(:,1:20),'noncoherent');
plot(rnggrid,abs(intpulse))
xlabel('Range (m)')
title('Noncoherent Integration of 20 Pulses')

Algorithms

Data Precision

This System object supports single and double precision for input data, properties, and arguments. If the input data X is single precision, the output data is single precision. If the input data X is double precision, the output data is double precision. The precision of the output is independent of the precision of the properties and other arguments.

References

[1] Richards, M. Fundamentals of Radar Signal Processing, 2nd ed. McGraw-Hill Professional Engineering, 2014.

[2] Richards, M., J. Scheer, and W. Holm, Principles of Modern Radar: Basic Principles. SciTech Publishing, 2010.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• The CustomRangeWindow property is not supported.

• The plotResponse method is not supported.

• See System Objects in MATLAB Code Generation (MATLAB Coder).

This System object supports single and double precision for input data, properties, and arguments. If the input data X is single precision, the output data is single precision. If the input data X is double precision, the output data is double precision. The precision of the output is independent of the precision of the properties and other arguments.

Version History

Introduced in R2017a