overshoot
Overshoot metrics of bilevel waveform transitions
Syntax
Description
[___] = overshoot(___,
specifies additional options using one or more Name,Value)Name,Value arguments.
You can use any of the output combinations from previous syntaxes.
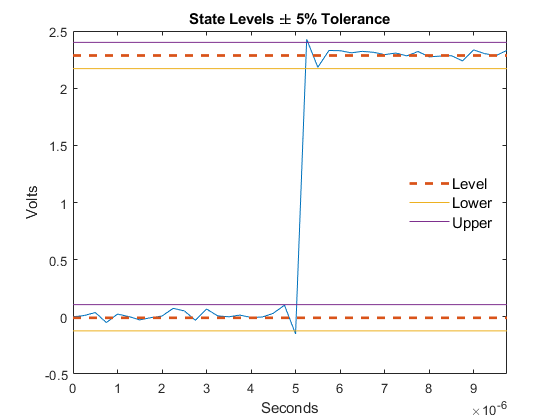
overshoot(___) plots the bilevel waveform and marks the
location of the overshoot of each transition. The function also plots the lower and upper
reference-level instants and associated reference levels and the state levels and associated
lower- and upper-state boundaries.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] IEEE Standard 181. IEEE® Standard on Transitions, Pulses, and Related Waveforms (2003): 15–17.
Extended Capabilities
Version History
Introduced in R2012a