parzenwin
Parzen (de la Vallée Poussin) window
Description
Examples
Input Arguments
Output Arguments
Algorithms
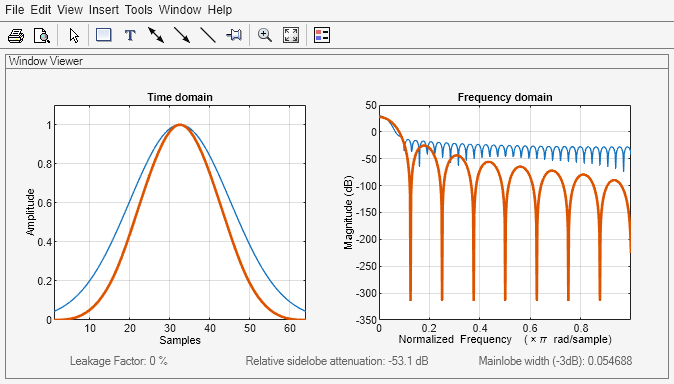
Parzen windows are piecewise-cubic approximations of Gaussian windows. Parzen window sidelobes fall off as 1/ω4.
This equation defines the N–point Parzen window over the
interval :
References
[1] Harris, Fredric J. "On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform." Proceedings of the IEEE®. Vol. 66, January 1978, pp. 51–83.
Extended Capabilities
Version History
Introduced before R2006aSee Also
Apps
Functions
barthannwin|bartlett|blackmanharris|bohmanwin|nuttallwin|rectwin|triang| WVTool