kfoldLoss
Classification loss for cross-validated classification model
Description
L = kfoldLoss(CVMdl)CVMdl. For every fold, kfoldLoss computes the
classification loss for validation-fold observations using a classifier trained on
training-fold observations. CVMdl.X and CVMdl.Y
contain both sets of observations.
L = kfoldLoss(CVMdl,Name,Value)
Examples
Load the ionosphere data set.
load ionosphereGrow a classification tree.
tree = fitctree(X,Y);
Cross-validate the classification tree using 10-fold cross-validation.
cvtree = crossval(tree);
Estimate the cross-validated classification error.
L = kfoldLoss(cvtree)
L = 0.1083
Load the ionosphere data set.
load ionosphereTrain a classification ensemble of 100 decision trees using AdaBoostM1. Specify tree stumps as the weak learners.
t = templateTree('MaxNumSplits',1); ens = fitcensemble(X,Y,'Method','AdaBoostM1','Learners',t);
Cross-validate the ensemble using 10-fold cross-validation.
cvens = crossval(ens);
Estimate the cross-validated classification error.
L = kfoldLoss(cvens)
L = 0.0655
Train a cross-validated generalized additive model (GAM) with 10 folds. Then, use kfoldLoss to compute cumulative cross-validation classification errors (misclassification rate in decimal). Use the errors to determine the optimal number of trees per predictor (linear term for predictor) and the optimal number of trees per interaction term.
Alternatively, you can find optimal values of fitcgam name-value arguments by using the OptimizeHyperparameters name-value argument. For an example, see Optimize GAM Using OptimizeHyperparameters.
Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').
load ionosphereCreate a cross-validated GAM by using the default cross-validation option. Specify the 'CrossVal' name-value argument as 'on'. Specify to include all available interaction terms whose p-values are not greater than 0.05.
rng('default') % For reproducibility CVMdl = fitcgam(X,Y,'CrossVal','on','Interactions','all','MaxPValue',0.05);
If you specify 'Mode' as 'cumulative' for kfoldLoss, then the function returns cumulative errors, which are the average errors across all folds obtained using the same number of trees for each fold. Display the number of trees for each fold.
CVMdl.NumTrainedPerFold
ans = struct with fields:
PredictorTrees: [65 64 59 61 60 66 65 62 64 61]
InteractionTrees: [1 2 2 2 2 1 2 2 2 2]
kfoldLoss can compute cumulative errors using up to 59 predictor trees and one interaction tree.
Plot the cumulative, 10-fold cross-validated, classification error (misclassification rate in decimal). Specify 'IncludeInteractions' as false to exclude interaction terms from the computation.
L_noInteractions = kfoldLoss(CVMdl,'Mode','cumulative','IncludeInteractions',false); figure plot(0:min(CVMdl.NumTrainedPerFold.PredictorTrees),L_noInteractions)

The first element of L_noInteractions is the average error over all folds obtained using only the intercept (constant) term. The (J+1)th element of L_noInteractions is the average error obtained using the intercept term and the first J predictor trees per linear term. Plotting the cumulative loss allows you to monitor how the error changes as the number of predictor trees in GAM increases.
Find the minimum error and the number of predictor trees used to achieve the minimum error.
[M,I] = min(L_noInteractions)
M = 0.0655
I = 23
The GAM achieves the minimum error when it includes 22 predictor trees.
Compute the cumulative classification error using both linear terms and interaction terms.
L = kfoldLoss(CVMdl,'Mode','cumulative')
L = 2×1
0.0712
0.0712
The first element of L is the average error over all folds obtained using the intercept (constant) term and all predictor trees per linear term. The second element of L is the average error obtained using the intercept term, all predictor trees per linear term, and one interaction tree per interaction term. The error does not decrease when interaction terms are added.
If you are satisfied with the error when the number of predictor trees is 22, you can create a predictive model by training the univariate GAM again and specifying 'NumTreesPerPredictor',22 without cross-validation.
Input Arguments
Cross-validated partitioned classifier, specified as a ClassificationPartitionedModel, ClassificationPartitionedEnsemble, or ClassificationPartitionedGAM object. You can create the object in two ways:
Pass a trained classification model listed in the following table to its
crossvalobject function.Train a classification model using a function listed in the following table and specify one of the cross-validation name-value arguments for the function.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: kfoldLoss(CVMdl,'Folds',[1 2 3 5]) specifies to use the
first, second, third, and fifth folds to compute the classification loss, but to exclude the
fourth fold.
Fold indices to use, specified as a positive integer vector. The elements of Folds must be within the range from 1 to CVMdl.KFold.
The software uses only the folds specified in Folds.
Example: 'Folds',[1 4 10]
Data Types: single | double
Flag to include interaction terms of the model, specified as true or
false. This argument is valid only for a generalized
additive model (GAM). That is, you can specify this argument only when
CVMdl is ClassificationPartitionedGAM.
The default value is true if the models in
CVMdl (CVMdl.Trained) contain
interaction terms. The value must be false if the models do not
contain interaction terms.
Data Types: logical
Loss function, specified as a built-in loss function name or a function handle.
The default loss function depends on the model type of CVMdl.
The default value is
'classiferror'if the model type is an ensemble or support vector machine classifier.The default value is
'mincost'if the model type is a discriminant analysis, k-nearest neighbor, naive Bayes, neural network, or tree classifier.If the model type is a generalized additive model classifier, the default value is
'mincost'if theScoreTransformproperty of the input model object (CVMdl.ScoreTransform'logit'; otherwise, the default value is'classiferror'.
'classiferror' and 'mincost' are
equivalent when you use the default cost matrix. See Algorithms for more information.
This table lists the available loss functions. Specify one using its corresponding character vector or string scalar.
Value Description 'binodeviance'Binomial deviance 'classifcost'Observed misclassification cost 'classiferror'Misclassified rate in decimal 'crossentropy'Cross-entropy loss (for neural networks only) 'exponential'Exponential loss 'hinge'Hinge loss 'logit'Logistic loss 'mincost'Minimal expected misclassification cost (for classification scores that are posterior probabilities) 'quadratic'Quadratic loss 'mincost'is appropriate for classification scores that are posterior probabilities. ThepredictandkfoldPredictfunctions of discriminant analysis, generalized additive model, k-nearest neighbor, naive Bayes, neural network, and tree classifiers return such scores by default.For ensemble models that use
'Bag'or'Subspace'methods, classification scores are posterior probabilities by default. For ensemble models that use'AdaBoostM1','AdaBoostM2',GentleBoost, or'LogitBoost'methods, you can use posterior probabilities as classification scores by specifying the double-logit score transform. For example, enter:For all other ensemble methods, the software does not support posterior probabilities as classification scores.CVMdl.ScoreTransform = 'doublelogit';For SVM models, you can specify to use posterior probabilities as classification scores by setting
'FitPosterior',truewhen you cross-validate the model usingfitcsvm.
Specify your own function using function handle notation.
Suppose that
nis the number of observations in the training data (CVMdl.NumObservations) andKis the number of classes (numel(CVMdl.ClassNames)). Your function must have the signaturelossvalue =, where:lossfun(C,S,W,Cost)The output argument
lossvalueis a scalar.You specify the function name (
lossfun).Cis ann-by-Klogical matrix with rows indicating the class to which the corresponding observation belongs. The column order corresponds to the class order inCVMdl.ClassNames.Construct
Cby settingC(p,q) = 1if observationpis in classq, for each row. Set all other elements of rowpto0.Sis ann-by-Knumeric matrix of classification scores. The column order corresponds to the class order inCVMdl.ClassNames. The inputSresembles the output argumentscoreofkfoldPredict.Wis ann-by-1 numeric vector of observation weights. If you passW, the software normalizes its elements to sum to1.Costis aK-by-Knumeric matrix of misclassification costs. For example,Cost = ones(K) – eye(K)specifies a cost of0for correct classification, and1for misclassification.
Specify your function using
'LossFun',@.lossfun
For more details on loss functions, see Classification Loss.
Example: 'LossFun','hinge'
Data Types: char | string | function_handle
Aggregation level for the output, specified as 'average', 'individual', or 'cumulative'.
| Value | Description |
|---|---|
'average' | The output is a scalar average over all folds. |
'individual' | The output is a vector of length k containing one value per fold, where k is the number of folds. |
'cumulative' | Note If you want to specify this value,
|
Example: 'Mode','individual'
Output Arguments
Classification loss, returned as a numeric scalar or numeric column vector.
If
Modeis'average', thenLis the average classification loss over all folds.If
Modeis'individual', thenLis a k-by-1 numeric column vector containing the classification loss for each fold, where k is the number of folds.If
Modeis'cumulative'andCVMdlisClassificationPartitionedEnsemble, thenLis amin(CVMdl.NumTrainedPerFold)-by-1 numeric column vector. Each elementjis the average classification loss over all folds that the function obtains by using ensembles trained with weak learners1:j.If
Modeis'cumulative'andCVMdlisClassificationPartitionedGAM, then the output value depends on theIncludeInteractionsvalue.If
IncludeInteractionsisfalse, thenLis a(1 + min(NumTrainedPerFold.PredictorTrees))-by-1 numeric column vector. The first element ofLis the average classification loss over all folds that is obtained using only the intercept (constant) term. The(j + 1)th element ofLis the average loss obtained using the intercept term and the firstjpredictor trees per linear term.If
IncludeInteractionsistrue, thenLis a(1 + min(NumTrainedPerFold.InteractionTrees))-by-1 numeric column vector. The first element ofLis the average classification loss over all folds that is obtained using the intercept (constant) term and all predictor trees per linear term. The(j + 1)th element ofLis the average loss obtained using the intercept term, all predictor trees per linear term, and the firstjinteraction trees per interaction term.
More About
Classification loss functions measure the predictive inaccuracy of classification models. When you compare the same type of loss among many models, a lower loss indicates a better predictive model.
Consider the following scenario.
L is the weighted average classification loss.
n is the sample size.
For binary classification:
yj is the observed class label. The software codes it as –1 or 1, indicating the negative or positive class (or the first or second class in the
ClassNamesproperty), respectively.f(Xj) is the positive-class classification score for observation (row) j of the predictor data X.
mj = yjf(Xj) is the classification score for classifying observation j into the class corresponding to yj. Positive values of mj indicate correct classification and do not contribute much to the average loss. Negative values of mj indicate incorrect classification and contribute significantly to the average loss.
For algorithms that support multiclass classification (that is, K ≥ 3):
yj* is a vector of K – 1 zeros, with 1 in the position corresponding to the true, observed class yj. For example, if the true class of the second observation is the third class and K = 4, then y2* = [
0 0 1 0]′. The order of the classes corresponds to the order in theClassNamesproperty of the input model.f(Xj) is the length K vector of class scores for observation j of the predictor data X. The order of the scores corresponds to the order of the classes in the
ClassNamesproperty of the input model.mj = yj*′f(Xj). Therefore, mj is the scalar classification score that the model predicts for the true, observed class.
The weight for observation j is wj. The software normalizes the observation weights so that they sum to the corresponding prior class probability stored in the
Priorproperty. Therefore,
Given this scenario, the following table describes the supported loss functions that you can specify by using the LossFun name-value argument.
| Loss Function | Value of LossFun | Equation |
|---|---|---|
| Binomial deviance | "binodeviance" | |
| Observed misclassification cost | "classifcost" | where is the class label corresponding to the class with the maximal score, and is the user-specified cost of classifying an observation into class when its true class is yj. |
| Misclassified rate in decimal | "classiferror" | where I{·} is the indicator function. |
| Cross-entropy loss | "crossentropy" |
The weighted cross-entropy loss is where the weights are normalized to sum to n instead of 1. |
| Exponential loss | "exponential" | |
| Hinge loss | "hinge" | |
| Logistic loss | "logit" | |
| Minimal expected misclassification cost | "mincost" |
The software computes the weighted minimal expected classification cost using this procedure for observations j = 1,...,n.
The weighted average of the minimal expected misclassification cost loss is |
| Quadratic loss | "quadratic" |
If you use the default cost matrix (whose element value is 0 for correct classification
and 1 for incorrect classification), then the loss values for
"classifcost", "classiferror", and
"mincost" are identical. For a model with a nondefault cost matrix,
the "classifcost" loss is equivalent to the "mincost"
loss most of the time. These losses can be different if prediction into the class with
maximal posterior probability is different from prediction into the class with minimal
expected cost. Note that "mincost" is appropriate only if classification
scores are posterior probabilities.
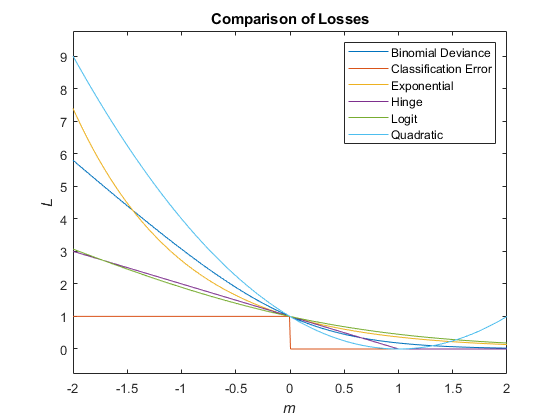
This figure compares the loss functions (except "classifcost",
"crossentropy", and "mincost") over the score
m for one observation. Some functions are normalized to pass through
the point (0,1).
Algorithms
kfoldLoss computes the classification loss as described in the
corresponding loss object function. For a model-specific description, see
the appropriate loss function reference page in the following
table.
| Model Type | loss Function |
|---|---|
| Discriminant analysis classifier | loss |
| Ensemble classifier | loss |
| Generalized additive model classifier | loss |
| k-nearest neighbor classifier | loss |
| Naive Bayes classifier | loss |
| Neural network classifier | loss |
| Support vector machine classifier | loss |
| Binary decision tree for multiclass classification | loss |
Extended Capabilities
Usage notes and limitations:
This function fully supports GPU arrays for the following cross-validated model objects:
Ensemble classifier trained with
fitcensemblek-nearest neighbor classifier trained with
fitcknnSupport vector machine classifier trained with
fitcsvmBinary decision tree for multiclass classification trained with
fitctreeNeural network for classification trained with
fitcnet
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2011akfoldLoss fully supports GPU arrays for ClassificationPartitionedModel models trained using
fitcnet.
Starting in R2023b, the following classification model object functions use observations with missing predictor values as part of resubstitution ("resub") and cross-validation ("kfold") computations for classification edges, losses, margins, and predictions.
In previous releases, the software omitted observations with missing predictor values from the resubstitution and cross-validation computations.
If you specify a nondefault cost matrix when you cross-validate the input model object for an SVM or ensemble classification model, the kfoldLoss function returns a different value compared to previous releases.
The kfoldLoss function uses the
observation weights stored in the W property. Also, the function uses the
cost matrix stored in the Cost property if you specify the
LossFun name-value argument as "classifcost" or
"mincost". The way the function uses the W and
Cost property values has not changed. However, the property values stored in the input model object have changed for
cross-validated SVM and ensemble model objects with a nondefault cost matrix, so the
function can return a different value.
For details about the property value change, see Cost property stores the user-specified cost matrix (cross-validated SVM classifier) or Cost property stores the user-specified cost matrix (cross-validated ensemble classifier).
If you want the software to handle the cost matrix, prior
probabilities, and observation weights in the same way as in previous releases, adjust the prior
probabilities and observation weights for the nondefault cost matrix, as described in Adjust Prior Probabilities and Observation Weights for Misclassification Cost Matrix. Then, when you train a
classification model, specify the adjusted prior probabilities and observation weights by using
the Prior and Weights name-value arguments, respectively,
and use the default cost matrix.
Starting in R2022a, the default value of the LossFun name-value
argument has changed for both a generalized additive model (GAM) and a neural network model,
so that the kfoldLoss function uses the "mincost"
option (minimal expected misclassification cost) as the default when a cross-validated
classification object uses posterior probabilities for classification scores.
If the model type of the input model object
CVMdlis a GAM classifier, the default value is"mincost"if theScoreTransformproperty ofCVMdl(CVMdl.ScoreTransform'logit'; otherwise, the default value is"classiferror".If the model type of
CVMdlis a neural network model classifier, the default value is"mincost".
In previous releases, the default value was
'classiferror'.
You do not need to make any changes to your code if you use the default cost matrix (whose element value is 0 for correct classification and 1 for incorrect classification). The "mincost" option is equivalent to the "classiferror" option for the default cost matrix.
See Also
ClassificationPartitionedModel | kfoldPredict | kfoldEdge | kfoldMargin | kfoldfun
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)