fitrqnet

Train regression quantile neural network

Since R2024b

Syntax

Mdl = fitrqnet(Tbl,ResponseVarName)

Mdl = fitrqnet(Tbl,formula)

Mdl = fitrqnet(Tbl,Y)

Mdl = fitrqnet(X,Y)

Mdl = fitrqnet(___,Name=Value)

Description

Mdl = fitrqnet(Tbl,ResponseVarName) returns a trained regression quantile neural network model Mdl. The function trains the model using the predictors in the table Tbl and the response values in the ResponseVarName table variable.

By default, the function uses the median (0.5 quantile).

Mdl = fitrqnet(Tbl,formula) returns a quantile neural network model trained using the sample data in the table Tbl. The input argument formula is an explanatory model of the response and a subset of the predictor variables in Tbl used to fit Mdl.

Mdl = fitrqnet(Tbl,Y) returns a quantile neural network model trained using the predictor variables in the table Tbl and the response values in the vector Y.

Mdl = fitrqnet(X,Y) returns a quantile neural network model trained using the predictors in the matrix X and the response values in the vector Y.

Mdl = fitrqnet(___,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. For example, you can specify the quantiles by using the Quantiles name-value argument.

Examples

Fit Quantile Neural Network Regression Model

Fit a quantile neural network regression model using the 0.25, 0.50, and 0.75 quantiles.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a matrix X containing the predictor variables Acceleration, Displacement, Horsepower, and Weight. Store the response variable MPG in the variable Y.

load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
Y = MPG;

Delete rows of X and Y where either array has missing values.

R = rmmissing([X Y]);
X = R(:,1:end-1);
Y = R(:,end);

Partition the data into training data (XTrain and YTrain) and test data (XTest and YTest). Reserve approximately 20% of the observations for testing, and use the rest of the observations for training.

rng(0,"twister") % For reproducibility of the partition
c = cvpartition(length(Y),"Holdout",0.20);
 
trainingIdx = training(c);
XTrain = X(trainingIdx,:);
YTrain = Y(trainingIdx);
 
testIdx = test(c);
XTest = X(testIdx,:);
YTest = Y(testIdx);

Train a quantile neural network regression model. Specify to use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, standardize the numeric predictors. Use a ridge (L2) regularization term of 1. Adding a regularization term can help prevent quantile crossing.

Mdl = fitrqnet(XTrain,YTrain,Quantiles=[0.25,0.50,0.75], ...
    Standardize=true,Lambda=0.05)

Mdl = 
  RegressionQuantileNeuralNetwork
             ResponseName: 'Y'
    CategoricalPredictors: []
               LayerSizes: 10
              Activations: 'relu'
    OutputLayerActivation: 'none'
                Quantiles: [0.2500 0.5000 0.7500]

Mdl is a RegressionQuantileNeuralNetwork model object. You can use dot notation to access the properties of Mdl. For example, Mdl.LayerWeights and Mdl.LayerBiases contain the weights and biases, respectively, for the fully connected layers of the trained model.

In this example, you can use the layer weights, layer biases, predictor means, and predictor standard deviations directly to predict the test set responses for each of the three quantiles in Mdl.Quantiles. In general, you can use the predict object function to make quantile predictions.

firstFCStep = (Mdl.LayerWeights{1})*((XTest-Mdl.Mu)./Mdl.Sigma)' ...
    + Mdl.LayerBiases{1};
reluStep = max(firstFCStep,0);
finalFCStep = (Mdl.LayerWeights{end})*reluStep + Mdl.LayerBiases{end};
predictedY = finalFCStep'

predictedY = 78×3

   13.9602   15.1340   16.6884
   11.2792   12.2332   13.4849
   19.5525   21.7303   23.9473
   22.6950   25.5260   28.1201
   10.4533   11.3377   12.4984
   17.6935   19.5194   21.5152
   12.4312   13.4797   14.8614
   11.7998   12.7963   14.1071
   16.6860   18.3305   20.2070
   24.1142   27.0301   29.7811
      ⋮

isequal(predictedY,predict(Mdl,XTest))

ans = logical
   1

Each column of predictedY corresponds to a separate quantile (0.25, 0.5, or 0.75).

Visualize the predictions of the quantile neural network regression model. First, create a grid of predictor values.

minX = floor(min(X))

minX = 1×4

           8          68          46        1613

maxX = ceil(max(X))

maxX = 1×4

          25         455         230        5140

gridX = zeros(100,size(X,2));
for p = 1:size(X,2)
    gridp = linspace(minX(p),maxX(p))';
    gridX(:,p) = gridp;
end

Next, use the trained model Mdl to predict the response values for the grid of predictor values.

gridY = predict(Mdl,gridX)

gridY = 100×3

   31.2419   35.0661   38.6357
   30.8637   34.6317   38.1573
   30.4854   34.1972   37.6789
   30.1072   33.7627   37.2005
   29.7290   33.3283   36.7221
   29.3507   32.8938   36.2436
   28.9725   32.4593   35.7652
   28.5943   32.0249   35.2868
   28.2160   31.5904   34.8084
   27.8378   31.1560   34.3300
      ⋮

For each observation in gridX, the predict object function returns predictions for the quantiles in Mdl.Quantiles.

View the gridY predictions for the second predictor (Displacement). Compare the quantile predictions to the true test data values.

predictorIdx = 2;
plot(XTest(:,predictorIdx),YTest,".")
hold on
plot(gridX(:,predictorIdx),gridY(:,1))
plot(gridX(:,predictorIdx),gridY(:,2))
plot(gridX(:,predictorIdx),gridY(:,3))
hold off
xlabel("Predictor (Displacement)")
ylabel("Response (MPG)")
legend(["True values","0.25 predicted values", ...
    "0.50 predicted values","0.75 predicted values"])
title("Test Data")

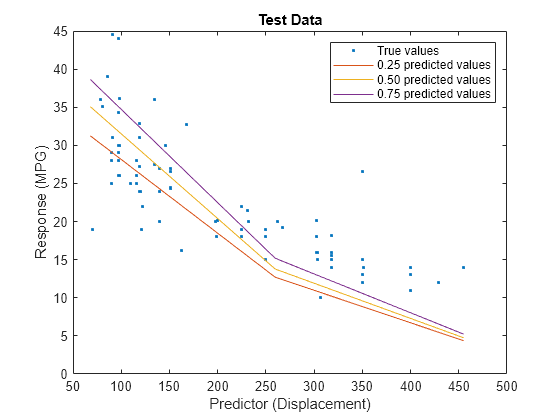
The red curve shows the predictions for the 0.25 quantile, the yellow curve shows the predictions for the 0.50 quantile, and the purple curve shows the predictions for the 0.75 quantile. The blue points indicate the true test data values.

Notice that the quantile prediction curves do not cross each other.

Prevent Quantile Crossing Using Regularization

When training a quantile neural network regression model, you can use a ridge (L2) regularization term to prevent quantile crossing.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Cylinders, Displacement, and so on, as well as the response variable MPG.

load carbig
cars = table(Acceleration,Cylinders,Displacement, ...
    Horsepower,Model_Year,Origin,Weight,MPG);

Remove rows of cars where the table has missing values.

cars = rmmissing(cars);

Categorize the cars based on whether they were made in the USA.

cars.Origin = categorical(cellstr(cars.Origin));
cars.Origin = mergecats(cars.Origin,["France","Japan",...
    "Germany","Sweden","Italy","England"],"NotUSA");

Partition the data into training and test sets using cvpartition. Use approximately 80% of the observations as training data, and 20% of the observations as test data.

rng(0,"twister") % For reproducibility of the data partition
c = cvpartition(height(cars),"Holdout",0.20);

trainingIdx = training(c);
carsTrain = cars(trainingIdx,:);

testIdx = test(c);
carsTest = cars(testIdx,:);

Train a quantile neural network regression model. Use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, standardize the numeric predictors before training.

Mdl = fitrqnet(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ...
    Standardize=true);

Mdl is a RegressionNeuralNetwork model object.

Determine if the test data predictions for the quantiles in Mdl.Quantiles cross each other by using the predict object function of Mdl. The crossingIndicator output argument contains a value of 1 (true) for any observation with quantile predictions that cross.

[~,crossingIndicator] = predict(Mdl,carsTest);
sum(crossingIndicator)

ans = 
2

In this example, two of the observations in carsTest have quantile predictions that cross each other.

To prevent quantile crossing, specify the Lambda name-value argument in the call to fitrqnet. Use a 0.05 ridge (L2) penalty term.

newMdl = fitrqnet(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ...
    Standardize=true,Lambda=0.05);
[predictedY,newCrossingIndicator] = predict(newMdl,carsTest);
sum(newCrossingIndicator)

ans = 
0

With regularization, the predictions for the test data set do not cross for any observations.

Visualize the predictions returned by newMdl by using a scatter plot with a reference line. Plot the predicted values along the vertical axis and the true response values along the horizontal axis. Points on the reference line indicate correct predictions.

plot(carsTest.MPG,predictedY(:,1),".")
hold on
plot(carsTest.MPG,predictedY(:,2),".")
plot(carsTest.MPG,predictedY(:,3),".")
plot(carsTest.MPG,carsTest.MPG)
hold off
xlabel("True MPG")
ylabel("Predicted MPG")
legend(["0.25 quantile values","0.50 quantile values", ...
    "0.75 quantile values","Reference line"], ...
    Location="southeast")
title("Test Data")

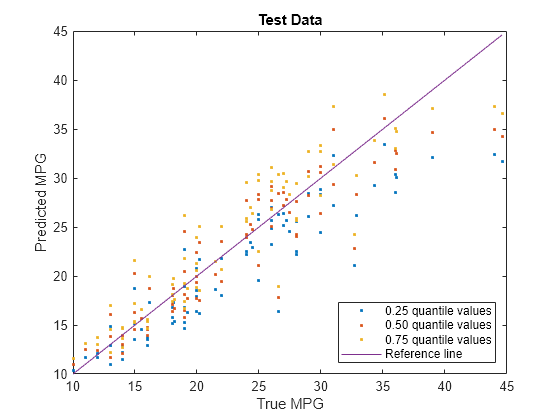
Blue points correspond to the 0.25 quantile, red points correspond to the 0.50 quantile, and yellow points correspond to the 0.75 quantile.

Input Arguments

Tbl — Sample data

table

Sample data used to train the model, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one predictor variable. Optionally, Tbl can contain one additional column for the response variable. Multicolumn variables and cell arrays other than cell arrays of character vectors are not allowed.

• If Tbl contains the response variable, and you want to use all remaining variables in Tbl as predictors, then specify the response variable by using ResponseVarName.

• If Tbl contains the response variable, and you want to use only a subset of the remaining variables in Tbl as predictors, then specify a formula by using formula.

• If Tbl does not contain the response variable, then specify a response variable by using Y. The length of the response variable and the number of rows in Tbl must be equal.

ResponseVarName — Response variable name

name of variable in Tbl

Response variable name, specified as the name of a variable in Tbl. The response variable must be a numeric vector.

You must specify ResponseVarName as a character vector or string scalar. For example, if Tbl stores the response variable Y as Tbl.Y, then specify it as "Y". Otherwise, the software treats all columns of Tbl, including Y, as predictors when training the model.

Data Types: char | string

formula — Explanatory model of response variable and subset of predictor variables

character vector | string scalar

Explanatory model of the response variable and a subset of the predictor variables, specified as a character vector or string scalar in the form "Y~x1+x2+x3". In this form, Y represents the response variable, and x1, x2, and x3 represent the predictor variables.

To specify a subset of variables in Tbl as predictors for training the model, use a formula. If you specify a formula, then the software does not use any variables in Tbl that do not appear in formula.

The variable names in the formula must be both variable names in Tbl (Tbl.Properties.VariableNames) and valid MATLAB^® identifiers. You can verify the variable names in Tbl by using the isvarname function. If the variable names are not valid, then you can convert them by using the matlab.lang.makeValidName function.

Data Types: char | string

Y — Response data

numeric vector

Response data, specified as a numeric vector. The length of Y must be equal to the number of observations in X or Tbl.

Data Types: single | double

X — Predictor data

numeric matrix

Predictor data used to train the model, specified as a numeric matrix.

By default, the software treats each row of X as one observation, and each column as one predictor.

The length of Y and the number of observations in X must be equal.

To specify the names of the predictors in the order of their appearance in X, use the PredictorNames name-value argument.

Note

If you orient your predictor matrix so that observations correspond to columns and specify ObservationsIn="columns", then you might experience a significant reduction in computation time.

Data Types: single | double

Note

The software treats NaN, empty character vector (''), empty string (""), <missing>, and <undefined> elements as missing values, and removes observations with any of these characteristics:

• Missing value in the response (for example, Y or ValidationData{2})

• At least one missing value in a predictor observation (for example, a row in X or ValidationData{1})

• NaN value or 0 weight (for example, a value in Weights or ValidationData{3})

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: fitrqnet(Tbl,"MPG",Quantiles=[0.25 0.5 0.75],Standardize=true) specifies to use the 0.25, 0.5, and 0.75 quantiles and to standardize the data before training.

Neural Network Options

Quantiles — Quantiles

0.5 (default) | vector of values in the range [0,1]

Quantiles to use for training Mdl, specified as a vector of values in the range [0,1]. The function trains a model that separates the bottom 100*q percent of training responses from the top 100*(1 – q) percent of training responses for each quantile q.

Example: Quantiles=[0.25 0.5 0.75]

Data Types: single | double

LayerSizes — Sizes of fully connected layers

10 (default) | positive integer vector

Sizes of the fully connected layers in the quantile neural network regression model, specified as a positive integer vector. Element i of LayerSizes is the number of outputs in the fully connected layer i of the neural network model.

LayerSizes does not include the size of the final fully connected layer. For more information, see Quantile Neural Network Structure.

Example: LayerSizes=[100 25 10]

Data Types: single | double

Activations — Activation functions for fully connected layers

"relu" (default) | "tanh" | "sigmoid" | "none" | string array | cell array of character vectors

Activation functions for the fully connected layers of the quantile neural network regression model, specified as a character vector, string scalar, string array, or cell array of character vectors with values from this table.

Value	Description
"relu"	Rectified linear unit (ReLU) function — Performs a threshold operation on each element of the input, where any value less than zero is set to zero, that is, $$f\left(x\right)=\{\begin{array}{cc}x,& x\ge 0\\ 0,& x<0\end{array}$$
"tanh"	Hyperbolic tangent (tanh) function — Applies the tanh function to each input element
"sigmoid"	Sigmoid function — Performs the following operation on each input element: $$f(x)=\frac{1}{1+e^{-x}}$$
"none"	Identity function — Returns each input element without performing any transformation, that is, f(x) = x

• If you specify one activation function only, then Activations is the activation function for every fully connected layer of the neural network model, excluding the final fully connected layer (see Quantile Neural Network Structure).

• If you specify an array of activation functions, then element i of Activations is the activation function for layer i of the neural network model.

Example: Activations="sigmoid"

Data Types: char | string | cell

LayerWeightsInitializer — Function to initialize fully connected layer weights

"glorot" (default) | "he"

Function to initialize the fully connected layer weights, specified as "glorot" or "he".

Value	Description
"glorot"	Initialize the weights with the Glorot initializer [1] (also known as the Xavier initializer). For each layer, the Glorot initializer independently samples from a uniform distribution with zero mean and variance 2/(I+O), where I is the input size and O is the output size for the layer.
"he"	Initialize the weights with the He initializer [2]. For each layer, the He initializer samples from a normal distribution with zero mean and variance 2/I, where I is the input size for the layer.

Example: LayerWeightsInitializer="he"

Data Types: char | string

LayerBiasesInitializer — Type of initial fully connected layer biases

"zeros" (default) | "ones"

Type of initial fully connected layer biases, specified as "zeros" or "ones".

• If you specify the value "zeros", then each fully connected layer has an initial bias of 0.

• If you specify the value "ones", then each fully connected layer has an initial bias of 1.

Example: LayerBiasesInitializer="ones"

Data Types: char | string

ObservationsIn — Predictor data observation dimension

"rows" (default) | "columns"

Predictor data observation dimension, specified as "rows" or "columns".

Note

If you orient your predictor matrix so that observations correspond to columns and specify ObservationsIn="columns", then you might experience a significant reduction in computation time. You cannot specify ObservationsIn="columns" for predictor data in a table.

Example: ObservationsIn="columns"

Data Types: char | string

Lambda — Regularization term strength

0 (default) | nonnegative scalar

Regularization term strength, specified as a nonnegative scalar. The software constructs the objective function for minimization from the quantile loss averaged over the quantiles (see Quantile Loss) and the ridge (L2) penalty term.

Example: Lambda=1e-4

Data Types: single | double

Standardize — Flag to standardize predictor data

false or 0 (default) | true or 1

Flag to standardize the predictor data, specified as a numeric or logical 0 (false) or 1 (true). If you set Standardize to true, then the software centers and scales each numeric predictor variable by the corresponding column mean and standard deviation. The software does not standardize categorical predictors.

Example: Standardize=true

Data Types: single | double | logical

Convergence Control Options

Verbose — Verbosity level

0 (default) | 1

Verbosity level, specified as 0 or 1. The Verbose name-value argument controls the display of diagnostic information at the command line.

Value	Description
0	fitrqnet does not display diagnostic information.
1	fitrqnet periodically displays diagnostic information.

fitrqnet stores the diagnostic information in Mdl. Use Mdl.ConvergenceInfo.History to access the diagnostic information.

Example: Verbose=1

Data Types: single | double

VerboseFrequency — Frequency of verbose printing

1 (default) | positive integer scalar

Frequency of verbose printing, which is the number of iterations between printing diagnostic information at the command line, specified as a positive integer scalar. A value of 1 indicates to print diagnostic information at every iteration.

Note

To use this name-value argument, you must set Verbose to 1.

Example: VerboseFrequency=5

Data Types: single | double

InitialStepSize — Initial step size

[] (default) | positive scalar | "auto"

Initial step size, specified as a positive scalar or "auto". By default, fitrqnet does not use the initial step size to determine the initial Hessian approximation used in training the model. However, if you specify an initial step size $${\Vert s_0\Vert }_{\infty }$$, then the initial inverse-Hessian approximation is $$\frac{{\Vert s_0\Vert }_{\infty }}{{\Vert \nabla {ℒ}_0\Vert }_{\infty }}I$$. $$\nabla {ℒ}_0$$ is the initial gradient vector, and $$I$$ is the identity matrix.

To have fitrqnet determine an initial step size automatically, specify the value as "auto". In this case, the function determines the initial step size by using $${\Vert s_0\Vert }_{\infty }=0.5{\Vert {\eta }_0\Vert }_{\infty }+0.1$$. $$s_0$$ is the initial step vector, and $${\eta }_0$$ is the vector of unconstrained initial weights and biases.

Example: InitialStepSize="auto"

Data Types: single | double | char | string

IterationLimit — Maximum number of training iterations

1e3 (default) | positive integer scalar

Maximum number of training iterations, specified as a positive integer scalar.

The software returns a trained model regardless of whether the training routine successfully converges. Mdl.ConvergenceInfo.ConvergenceCriterion contains convergence information.

Example: IterationLimit=1e8

Data Types: single | double

GradientTolerance — Relative gradient tolerance

1e-6 (default) | nonnegative scalar

Relative gradient tolerance, specified as a nonnegative scalar.

Let $${ℒ}_t$$ be the loss function at training iteration t, $$\nabla {ℒ}_t$$ be the gradient of the loss function with respect to the weights and biases at iteration t, and $$\nabla {ℒ}_0$$ be the gradient of the loss function at an initial point. If $$\max \left|\nabla {ℒ}_t\right|\le a\cdot \text{GradientTolerance}$$, where $$a=\max \left(1,\min \left|{ℒ}_t\right|,\max \left|\nabla {ℒ}_0\right|\right)$$, then the training process terminates.

Example: GradientTolerance=1e-5

Data Types: single | double

LossTolerance — Loss tolerance

1e-6 (default) | nonnegative scalar

Loss tolerance, specified as a nonnegative scalar.

If the function loss at some iteration is smaller than LossTolerance, then the training process terminates.

Example: LossTolerance=1e-8

Data Types: single | double

StepTolerance — Step size tolerance

1e-6 (default) | nonnegative scalar

Step size tolerance, specified as a nonnegative scalar.

If the step size at some iteration is smaller than StepTolerance, then the training process terminates.

Example: StepTolerance=1e-4

Data Types: single | double

ValidationData — Validation data for training convergence detection

cell array | table

Validation data for training convergence detection, specified as a cell array or a table.

During the training process, the software periodically estimates the validation loss by using ValidationData. If the validation loss increases more than ValidationPatience times consecutively, then the software terminates the training.

You can specify ValidationData as a table if you use a table Tbl of predictor data that contains the response variable. In this case, ValidationData must contain the same predictors and response contained in Tbl. The software does not apply weights to observations, even if Tbl contains a vector of weights. To specify weights, you must specify ValidationData as a cell array.

If you specify ValidationData as a cell array, then it must have the following format:

• ValidationData{1} must have the same data type and orientation as the predictor data. That is, if you use a predictor matrix X, then ValidationData{1} must be an m-by-p or p-by-m matrix of predictor data that has the same orientation as X. The predictor variables in the training data X and ValidationData{1} must correspond. Similarly, if you use a predictor table Tbl of predictor data, then ValidationData{1} must be a table containing the same predictor variables contained in Tbl. The number of observations in ValidationData{1} and the predictor data can vary.

• ValidationData{2} must match the data type and format of the response variable, either Y or ResponseVarName. If ValidationData{2} is an array of responses, then it must have the same number of elements as the number of observations in ValidationData{1}. If ValidationData{1} is a table, then ValidationData{2} can be the name of the response variable in the table. If you want to use the same ResponseVarName or formula, you can specify ValidationData{2} as [].

• Optionally, you can specify ValidationData{3} as an m-dimensional numeric vector of observation weights or the name of a variable in the table ValidationData{1} that contains observation weights. The software normalizes the weights with the validation data so that they sum to 1.

If you specify ValidationData and want to display the validation loss at the command line, set Verbose to 1.

Data Types: table | cell

ValidationFrequency — Number of iterations between validation evaluations

1 (default) | positive integer scalar

Number of iterations between validation evaluations, specified as a positive integer scalar. A value of 1 indicates to evaluate validation metrics at every iteration.

Note

To use this name-value argument, you must specify ValidationData.

Example: ValidationFrequency=5

Data Types: single | double

ValidationPatience — Stopping condition for validation evaluations

6 (default) | nonnegative integer scalar

Stopping condition for validation evaluations, specified as a nonnegative integer scalar. Training stops if the validation loss is greater than or equal to the minimum validation loss computed so far, ValidationPatience times consecutively. You can check the Mdl.ConvergenceInfo.History table to see the running total of times that the validation loss is greater than or equal to the minimum (Validation Checks).

Example: ValidationPatience=10

Data Types: single | double

Other Regression Options

CategoricalPredictors — Categorical predictors list

vector of positive integers | logical vector | character matrix | string array | cell array of character vectors | "all"

Categorical predictors list, specified as one of the values in this table. The descriptions assume that the predictor data has observations in rows and predictors in columns.

Value	Description
Vector of positive integers	Each entry in the vector is an index value indicating that the corresponding predictor is categorical. The index values are between 1 and p, where p is the number of predictors used to train the model. If fitrqnet uses a subset of input variables as predictors, then the function indexes the predictors using only the subset. The CategoricalPredictors values do not count any response variable, observation weights variable, or other variable that the function does not use.
Logical vector	A true entry means that the corresponding predictor is categorical. The length of the vector is p.
Character matrix	Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length.
String array or cell array of character vectors	Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames.
"all"	All predictors are categorical.

By default, if the predictor data is in a table (Tbl), fitrqnet assumes that a variable is categorical if it is a logical vector, categorical vector, character array, string array, or cell array of character vectors. If the predictor data is a matrix (X), fitrqnet assumes that all predictors are continuous. To identify any other predictors as categorical predictors, specify them by using the CategoricalPredictors name-value argument.

For the identified categorical predictors, fitrqnet creates dummy variables using two different schemes, depending on whether a categorical variable is unordered or ordered. For an unordered categorical variable, fitrqnet creates one dummy variable for each level of the categorical variable. For an ordered categorical variable, fitrqnet creates one less dummy variable than the number of categories. For details, see Automatic Creation of Dummy Variables.

Example: CategoricalPredictors="all"

Data Types: single | double | logical | char | string | cell

PredictorNames — Predictor variable names

string array of unique names | cell array of unique character vectors

Predictor variable names, specified as a string array of unique names or cell array of unique character vectors. The functionality of PredictorNames depends on the way you supply the training data.

• If you supply X and Y, then you can use PredictorNames to assign names to the predictor variables in X.

  • The order of the names in PredictorNames must correspond to the predictor order in X. Assuming that X has the default orientation, with observations in rows and predictors in columns, PredictorNames{1} is the name of X(:,1), PredictorNames{2} is the name of X(:,2), and so on. Also, size(X,2) and numel(PredictorNames) must be equal.

  • By default, PredictorNames is {'x1','x2',...}.

• If you supply Tbl, then you can use PredictorNames to choose which predictor variables to use in training. That is, fitrqnet uses only the predictor variables in PredictorNames and the response variable during training.

  • PredictorNames must be a subset of Tbl.Properties.VariableNames and cannot include the name of the response variable.

  • By default, PredictorNames contains the names of all predictor variables.

  • A good practice is to specify the predictors for training using either PredictorNames or formula, but not both.

Example: PredictorNames=["SepalLength","SepalWidth","PetalLength","PetalWidth"]

Data Types: string | cell

ResponseName — Response variable name

"Y" (default) | character vector | string scalar

Response variable name, specified as a character vector or string scalar.

• If you supply Y, then you can use ResponseName to specify a name for the response variable.

• If you supply ResponseVarName or formula, then you cannot use ResponseName.

Example: ResponseName="response"

Data Types: char | string

ResponseTransform — Function for transforming raw response values

"none" (default) | function handle | function name

Function for transforming raw response values, specified as a function handle or function name. The default is "none", which means @(y)y, or no transformation. The function should accept a vector (the original response values) and return a vector of the same size (the transformed response values).

Example: Suppose you create a function handle that applies an exponential transformation to an input vector by using myfunction = @(y)exp(y). Then, you can specify the response transformation as ResponseTransform=myfunction.

Data Types: char | string | function_handle

Weights — Observation weights

nonnegative numeric vector | name of variable in Tbl

Observation weights, specified as a nonnegative numeric vector or the name of a variable in Tbl. The software weights each observation in X or Tbl with the corresponding value in Weights. The length of Weights must equal the number of observations in X or Tbl.

If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if the weights vector W is stored as Tbl.W, then specify it as "W". Otherwise, the software treats all columns of Tbl, including W, as predictors when training the model.

By default, Weights is ones(n,1), where n is the number of observations in X or Tbl.

fitrqnet normalizes the weights to sum to 1.

Data Types: single | double | char | string

Output Arguments

Mdl — Trained quantile neural network model

RegressionQuantileNeuralNetwork model object

Trained quantile neural network model, returned as a RegressionQuantileNeuralNetwork model object.

To reference properties of Mdl, use dot notation.

More About

Quantile Neural Network Structure

The default quantile neural network regression model has the following layer structure.

Structure	Description
	Input — This layer corresponds to the predictor data in Tbl or X.
	First fully connected layer — This layer has 10 outputs, by default. You can widen the layer or add more fully connected layers to the network by specifying the LayerSizes name-value argument. You can find the weights and biases for this layer in the Mdl.LayerWeights{1} and Mdl.LayerBiases{1} properties of Mdl, respectively.
	ReLU activation function — fitrqnet applies this activation function to the first fully connected layer. You can change the activation function by specifying the Activations name-value argument.
	Final fully connected layer — This layer has one output for each quantile specified by the Quantiles name-value argument. You can find the weights and biases for this layer in the Mdl.LayerWeights{end} and Mdl.LayerBiases{end} properties of Mdl, respectively.
	Output — This layer corresponds to the predicted response values.

Tips

• You can use the α/2 and 1 – α/2 quantiles to create a prediction interval that captures an estimated 100*(1 – α) percent of the variation in the response.

Algorithms

Training Solver

fitrqnet uses a limited-memory Broyden-Fletcher-Goldfarb-Shanno quasi-Newton algorithm (LBFGS) [3] as its loss function minimization technique, where the software minimizes the quantile loss averaged over the quantiles (see Quantile Loss). The LBFGS solver uses a standard line-search method with an approximation to the Hessian.

Version History

Introduced in R2024b