loss
Loss of ECOC incremental learning classification model on batch of data
Since R2022a
Description
loss returns the classification loss of a configured
multiclass error-correcting output codes (ECOC) classification model for incremental learning
(incrementalClassificationECOC object).
To measure model performance on a data stream and store the results in the output model,
call updateMetrics or
updateMetricsAndFit.
Examples
The performance of an incremental model on streaming data is measured in three ways:
Cumulative metrics measure the performance since the start of incremental learning.
Window metrics measure the performance on a specified window of observations. The metrics are updated every time the model processes the specified window.
The
lossfunction measures the performance on a specified batch of data only.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Create an ECOC classification model for incremental learning. Specify the class names and a metrics window size of 1000 observations. Configure the model for loss by fitting it to the first 10 observations.
Mdl = incrementalClassificationECOC(ClassNames=unique(Y),MetricsWindowSize=1000); initobs = 10; Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));
Mdl is an incrementalClassificationECOC model. All its properties are read-only.
Simulate a data stream, and perform the following actions on each incoming chunk of 100 observations:
Call
updateMetricsto measure the cumulative performance and the performance within a window of observations. Overwrite the previous incremental model with a new one to track performance metrics.Call
lossto measure the model performance on the incoming chunk.Call
fitto fit the model to the incoming chunk. Overwrite the previous incremental model with a new one fitted to the incoming observations.Store all performance metrics to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 100; nchunk = floor((n - initobs)/numObsPerChunk); mc = array2table(zeros(nchunk,3),VariableNames=["Cumulative","Window","Chunk"]); % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); mc{j,["Cumulative","Window"]} = Mdl.Metrics{"ClassificationError",:}; mc{j,"Chunk"} = loss(Mdl,X(idx,:),Y(idx)); Mdl = fit(Mdl,X(idx,:),Y(idx)); end
Mdl is an incrementalClassificationECOC model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetrics checks the performance of the model on the incoming observations, and then the fit function fits the model to those observations. loss is agnostic of the metrics warm-up period, so it measures the classification error for every chunk.
To see how the performance metrics evolve during training, plot them.
plot(mc.Variables) xlim([0 nchunk]) ylabel("Classification Error") xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--") grid on legend(mc.Properties.VariableNames) xlabel("Iteration")
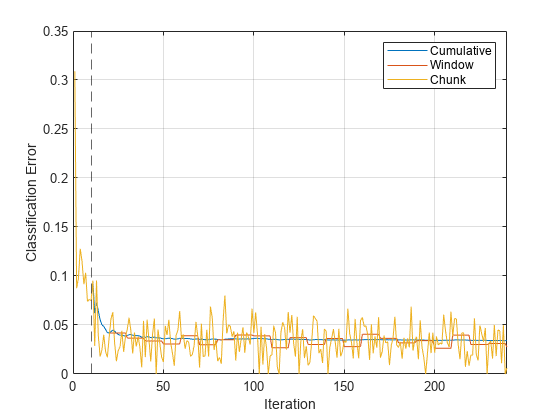
The yellow line represents the classification error on each incoming chunk of data. After the metrics warm-up period, Mdl tracks the cumulative and window metrics.
Fit an ECOC classification model for incremental learning to streaming data, and compute the minimum average binary loss on the incoming chunks of data.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Create an ECOC classification model for incremental learning. Configure the model as follows:
Specify the class names.
Specify a metrics warm-up period of 1000 observations.
Specify a metrics window size of 2000 observations.
Track the minimal average binary loss to measure the performance of the model. Create an anonymous function that measures the minimal average binary loss of each new observation. Create a structure array containing the name
MinimalLossand its corresponding function handle.Compute the classification loss by fitting the model to the first 10 observations.
tolerance = 1e-10; minimalBinaryLoss = @(~,S,~)min(-S,[],2); ce = struct("MinimalLoss",minimalBinaryLoss); Mdl = incrementalClassificationECOC(ClassNames=unique(Y), ... MetricsWarmupPeriod=1000,MetricsWindowSize=2000, ... Metrics=ce); initobs = 10; Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));
Mdl is an incrementalClassificationECOC model object configured for incremental learning.
Perform incremental learning. At each iteration:
Simulate a data stream by processing a chunk of 100 observations.
Call
updateMetricsto compute cumulative and window metrics on the incoming chunk of data. Overwrite the previous incremental model with a new one fitted to overwrite the previous metrics.Call
lossto compute the minimum average binary loss on the incoming chunk of data. Whereas the cumulative and window metrics require that custom losses return the loss for each observation,lossrequires the loss for the entire chunk. Compute the mean of the losses within a chunk.Call
fitto fit the incremental model to the incoming chunk of data.Store the cumulative, window, and chunk metrics to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 100; nchunk = floor((n - initobs)/numObsPerChunk); tanloss = array2table(zeros(nchunk,3), ... VariableNames=["Cumulative","Window","Chunk"]); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); tanloss{j,1:2} = Mdl.Metrics{"MinimalLoss",:}; tanloss{j,3} = loss(Mdl,X(idx,:),Y(idx), ... LossFun=@(z,zfit,w)mean(minimalBinaryLoss(z,zfit,w))); Mdl = fit(Mdl,X(idx,:),Y(idx)); end
Mdl is an incrementalClassificationECOC model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetrics checks the performance of the model on the incoming observations, and then the fit function fits the model to those observations.
Plot the performance metrics to see how they evolve during incremental learning.
semilogy(tanloss.Variables) xlim([0 nchunk]) ylabel("Minimal Average Binary Loss") xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"-.") xlabel("Iteration") legend(tanloss.Properties.VariableNames)
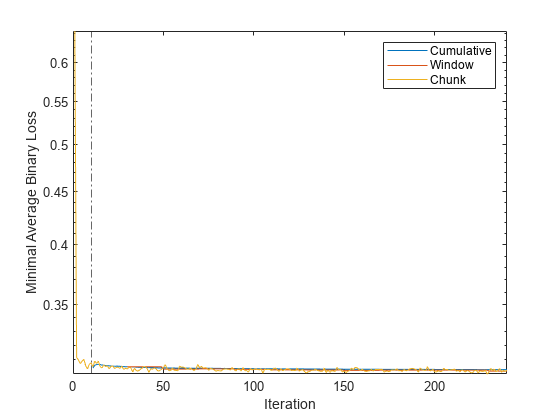
The plot suggests the following:
updateMetricscomputes the performance metrics after the metrics warm-up period only.updateMetricscomputes the cumulative metrics during each iteration.updateMetricscomputes the window metrics after processing 2000 observations (20 iterations).Because
Mdlis configured to predict observations from the beginning of incremental learning,losscan compute the minimum average binary loss on each incoming chunk of data.
Input Arguments
ECOC classification model for incremental learning, specified as an incrementalClassificationECOC model object. You can create
Mdl by calling
incrementalClassificationECOC directly, or by converting a
supported, traditionally trained machine learning model using the incrementalLearner function.
You must configure Mdl to predict labels for a batch of observations.
If
Mdlis a converted, traditionally trained model, you can predict labels without any modifications.Otherwise, you must fit
Mdlto data usingfitorupdateMetricsAndFit.
Batch of predictor data, specified as a floating-point matrix of
n observations and Mdl.NumPredictors predictor
variables. The value of the ObservationsIn name-value
argument determines the orientation of the variables and observations. The default
ObservationsIn value is "rows", which indicates that
observations in the predictor data are oriented along the rows of
X.
The length of the observation labels Y and the number of observations in X must be equal; Y( is the label of observation j (row or column) in j)X.
Note
loss supports only floating-point
input predictor data. If your input data includes categorical data, you must prepare an encoded
version of the categorical data. Use dummyvar to convert each categorical variable
to a numeric matrix of dummy variables. Then, concatenate all dummy variable matrices and any
other numeric predictors. For more details, see Dummy Variables.
Data Types: single | double
Batch of labels, specified as a categorical, character, or string array, a logical or floating-point vector, or a cell array of character vectors.
The length of the observation labels Y and the number of
observations in X must be equal;
Y( is the label of observation
j (row or column) in j)X.
If Y contains a label that is not a member of
Mdl.ClassNames, the loss function
issues an error. The data type of Y and
Mdl.ClassNames must be the same.
Data Types: char | string | cell | categorical | logical | single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: BinaryLoss="quadratic",Decoding="lossbased" specifies the
quadratic binary learner loss function and the loss-based decoding scheme for aggregating
the binary losses.
Binary learner loss function, specified as a built-in loss function name or function handle.
This table describes the built-in functions, where yj is the class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss formula.
Value Description Score Domain g(yj,sj) "binodeviance"Binomial deviance (–∞,∞) log[1 + exp(–2yjsj)]/[2log(2)] "exponential"Exponential (–∞,∞) exp(–yjsj)/2 "hamming"Hamming [0,1] or (–∞,∞) [1 – sign(yjsj)]/2 "hinge"Hinge (–∞,∞) max(0,1 – yjsj)/2 "linear"Linear (–∞,∞) (1 – yjsj)/2 "logit"Logistic (–∞,∞) log[1 + exp(–yjsj)]/[2log(2)] "quadratic"Quadratic [0,1] [1 – yj(2sj – 1)]2/2 The software normalizes binary losses so that the loss is 0.5 when yj = 0. Also, the software calculates the mean binary loss for each class [1].
For a custom binary loss function, for example
customFunction, specify its function handleBinaryLoss=@customFunction.customFunctionhas this form:bLoss = customFunction(M,s)
Mis the K-by-B coding matrix stored inMdl.CodingMatrix.sis the 1-by-B row vector of classification scores.bLossis the classification loss. This scalar aggregates the binary losses for every learner in a particular class. For example, you can use the mean binary loss to aggregate the loss over the learners for each class.K is the number of classes.
B is the number of binary learners.
For an example of a custom binary loss function, see Predict Test-Sample Labels of ECOC Model Using Custom Binary Loss Function. This example is for a traditionally trained model. You can define a custom loss function for incremental learning as shown in the example.
For more information, see Binary Loss.
Data Types: char | string | function_handle
Decoding scheme, specified as "lossweighted" or
"lossbased".
The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation. The software supports two decoding schemes:
"lossweighted"— The predicted class of an observation corresponds to the class that produces the minimum sum of the binary losses over binary learners."lossbased"— The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over binary learners.
For more information, see Binary Loss.
Example: Decoding="lossbased"
Data Types: char | string
Loss function, specified as "classiferror" (classification error)
or a function handle for a custom loss function.
To specify a custom loss function, use function handle notation. The function must have this form:
lossval = lossfcn(C,S,W)
The output argument
lossvalis an n-by-1 floating-point vector, where n is the number of observations inX. The value inlossval(is the classification loss of observationj)jYou specify the function name (
lossfcnCis an n-by-K logical matrix with rows indicating the class to which the corresponding observation belongs.Kis the number of distinct classes (numel(Mdl.ClassNames), and the column order corresponds to the class order in theClassNamesproperty. CreateCby settingC(=p,q)1, if observationpqp0.Sis an n-by-K numeric matrix of predicted classification scores.Sis similar to theNegLossoutput ofpredict, where rows correspond to observations in the data and the column order corresponds to the class order in theClassNamesproperty.S(is the classification score of observationp,q)pqWis an n-by-1 numeric vector of observation weights.
Example: LossFun=@lossfcn
Data Types: char | string | function_handle
Predictor data observation dimension, specified as "rows" or
"columns".
Example: ObservationsIn="columns"
Data Types: char | string
Batch of observation weights, specified as a floating-point vector of positive values. loss weighs the observations in the input data with the corresponding values in Weights. The size of Weights must equal n, which is the number of observations in the input data.
By default, Weights is ones(.n,1)
For more details, see Observation Weights.
Example: Weights=W specifies the observation weights as the vector
W.
Data Types: double | single
Output Arguments
Classification loss, returned as a numeric scalar. L is a measure
of model quality. Its interpretation depends on the loss function and weighting
scheme.
More About
The classification error has the form
where:
wj is the weight for observation j. The software renormalizes the weights to sum to 1.
ej = 1 if the predicted class of observation j differs from its true class, and 0 otherwise.
In other words, the classification error is the proportion of observations misclassified by the classifier.
The binary loss is a function of the class and classification score that determines how well a binary learner classifies an observation into the class. The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation.
Assume the following:
mkj is element (k,j) of the coding design matrix M—that is, the code corresponding to class k of binary learner j. M is a K-by-B matrix, where K is the number of classes, and B is the number of binary learners.
sj is the score of binary learner j for an observation.
g is the binary loss function.
is the predicted class for the observation.
The software supports two decoding schemes:
Loss-based decoding [2] (
Decodingis"lossbased") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over all binary learners.Loss-weighted decoding [3] (
Decodingis"lossweighted") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over the binary learners for the corresponding class.The denominator corresponds to the number of binary learners for class k. [1] suggests that loss-weighted decoding improves classification accuracy by keeping loss values for all classes in the same dynamic range.
The predict, resubPredict, and
kfoldPredict functions return the negated value of the objective
function of argmin as the second output argument
(NegLoss) for each observation and class.
This table summarizes the supported binary loss functions, where yj is a class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss function.
| Value | Description | Score Domain | g(yj,sj) |
|---|---|---|---|
"binodeviance" | Binomial deviance | (–∞,∞) | log[1 + exp(–2yjsj)]/[2log(2)] |
"exponential" | Exponential | (–∞,∞) | exp(–yjsj)/2 |
"hamming" | Hamming | [0,1] or (–∞,∞) | [1 – sign(yjsj)]/2 |
"hinge" | Hinge | (–∞,∞) | max(0,1 – yjsj)/2 |
"linear" | Linear | (–∞,∞) | (1 – yjsj)/2 |
"logit" | Logistic | (–∞,∞) | log[1 + exp(–yjsj)]/[2log(2)] |
"quadratic" | Quadratic | [0,1] | [1 – yj(2sj – 1)]2/2 |
The software normalizes binary losses so that the loss is 0.5 when yj = 0, and aggregates using the average of the binary learners [1].
Do not confuse the binary loss with the overall classification loss (specified by the
LossFun name-value argument of the loss and
predict object functions), which measures how well an ECOC classifier
performs as a whole.
Algorithms
If the prior class probability distribution is known (in other words, the prior distribution is not empirical), loss normalizes observation weights to sum to the prior class probabilities in the respective classes. This action implies that the default observation weights are the respective prior class probabilities.
If the prior class probability distribution is empirical, the software normalizes the specified observation weights to sum to 1 each time you call loss.
References
[1] Allwein, E., R. Schapire, and Y. Singer. “Reducing multiclass to binary: A unifying approach for margin classifiers.” Journal of Machine Learning Research. Vol. 1, 2000, pp. 113–141.
[2] Escalera, S., O. Pujol, and P. Radeva. “Separability of ternary codes for sparse designs of error-correcting output codes.” Pattern Recog. Lett. Vol. 30, Issue 3, 2009, pp. 285–297.
[3] Escalera, S., O. Pujol, and P. Radeva. “On the decoding process in ternary error-correcting output codes.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 32, Issue 7, 2010, pp. 120–134.
Extended Capabilities
Usage notes and limitations:
Use
saveLearnerForCoder,loadLearnerForCoder, andcodegen(MATLAB Coder) to generate code for thelossfunction. Save a trained model by usingsaveLearnerForCoder. Define an entry-point function that loads the saved model by usingloadLearnerForCoderand calls thelossfunction. Then usecodegento generate code for the entry-point function.To generate single-precision C/C++ code for
loss, specifyDataType="single"when you call theloadLearnerForCoderfunction.Use a homogeneous data type for all floating-point input arguments and object properties, specifically, either
singleordouble.This table contains notes about the arguments of
loss. Arguments not included in this table are fully supported.Argument Notes and Limitations MdlFor usage notes and limitations of the model object, see
incrementalClassificationECOC.XBatch-to-batch, the number of observations can be a variable size, but must equal the number of observations in
Y.The number of predictor variables must equal
Mdl.NumPredictors.Xmust besingleordouble.
YBatch-to-batch, the number of observations can be a variable size, but must equal the number of observations in
X.For classification problems, all labels in
Ymust be included inMdl.ClassNames.YandMdl.ClassNamesmust have the same data type.
"LossFun"The specified function cannot be an anonymous function.
For more information, see Introduction to Code Generation.
Version History
Introduced in R2022a
See Also
Functions
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)