fcontour

Plot contours

Syntax

fcontour(f)

fcontour(f,[min max])

fcontour(f,[xmin xmax ymin ymax])

fcontour(___,LineSpec)

fcontour(___,Name,Value)

fcontour(ax,___)

fc = fcontour(___)

Description

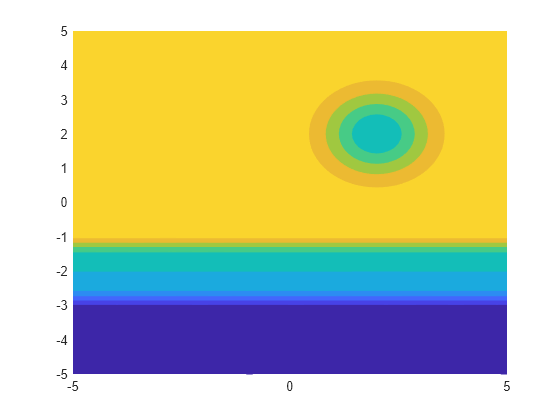
fcontour(f) plots the contour lines of symbolic expression f(x,y) over the default interval of x and y, which is [-5 5].

fcontour(f,[min max]) plots f over the interval min < x < max and min < y < max.

fcontour(f,[xmin xmax ymin ymax]) plots f over the interval xmin < x < xmax and ymin < y < ymax. The fcontour function uses symvar to order the variables and assign intervals.

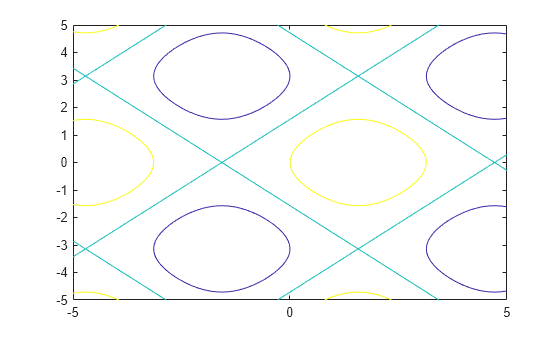
fcontour(___,LineSpec) uses LineSpec to set the line style and color. fcontour doesn’t support markers.

fcontour(___,Name,Value) specifies line properties using one or more Name,Value pair arguments. Use this option with any of the input argument combinations in the previous syntaxes. Name,Value pair settings apply to all the lines plotted. To set options for individual plots, use the objects returned by fcontour.

fcontour(ax,___) plots into the axes object ax instead of the current axes object gca.

fc = fcontour(___) returns a function contour object. Use the object to query and modify properties of a specific contour plot. For details, see FunctionContour Properties.

Examples

Plot Contours of Symbolic Expression

Plot the contours of $$\sin (x)+\cos (y)$$ over the default range of $$-5<x<5$$ and $$-5<y<5$$. Show the colorbar. Find a contour's level by matching the contour's color with the colorbar value.

syms x y
fcontour(sin(x) + cos(y))
colorbar

Plot Contours of Symbolic Function

Plot the contours of $$f(x,y)=\sin (x)+\cos (y)$$ over the default range of $$-5<x<5$$ and $$-5<y<5$$.

syms f(x,y)
f(x,y) = sin(x) + cos(y);
fcontour(f)

Specify Plotting Interval

Plot $$\sin (x)+\cos (y)$$ over $$-\pi /2<x<\pi /2$$ and $$0<y<5$$ by specifying the plotting interval as the second argument of fcontour.

syms x y
f = sin(x) + cos(y);
fcontour(f,[-pi/2 pi/2 0 5])

Change Line Style, Color and Width

Plot the contours of $$x^2-y^2$$ as blue, dashed lines by specifying the LineSpec input. Specify a LineWidth of 2. Markers are not supported by fcontour.

syms x y
fcontour(x^2 - y^2,'--b','LineWidth',2)

Plot Multiple Contour Plots on Same Figure

Plot multiple contour plots either by passing the inputs as a vector or by using hold on to successively plot on the same figure. If you specify LineStyle and Name-Value arguments, they apply to all contour plots. You cannot specify individual LineStyle and Name-Value pair arguments for each plot.

Divide a figure into two subplots by using subplot. On the first subplot, plot $$\sin (x)+\cos (y)$$ and $$x-y$$ by using vector input. On the second subplot, plot the same expressions by using hold on.

syms x y
subplot(2,1,1)
fcontour([sin(x)+cos(y) x-y])
title('Multiple Contour Plots Using Vector Inputs')

subplot(2,1,2)
fcontour(sin(x)+cos(y))
hold on
fcontour(x-y)
title('Multiple Contour Plots Using Hold Command')

hold off

Modify Contour Plot After Creation

Plot the contours of $$e^{-(x/3{)}^2-(y/3{)}^2}+e^{-(x+2{)}^2-(y+2{)}^2}$$. Specify an output to make fcontour return the plot object.

syms x y
f = exp(-(x/3)^2-(y/3)^2) + exp(-(x+2)^2-(y+2)^2);
fc = fcontour(f)

fc = 
  FunctionContour with properties:

     Function: exp(- x^2/9 - y^2/9) + exp(- (x + 2)^2 - (y + 2)^2)
    LineColor: 'flat'
    LineStyle: '-'
    LineWidth: 0.5000
         Fill: off
    LevelList: [0.2000 0.4000 0.6000 0.8000 1 1.2000 1.4000]

  Show all properties

Change the LineWidth to 1 and the LineStyle to a dashed line by using dot notation to set properties of the object fc. Visualize contours close to 0 and 1 by setting LevelList to [1 0.9 0.8 0.2 0.1].

fc.LineStyle = '--';
fc.LineWidth = 1;
fc.LevelList = [1 0.9 0.8 0.2 0.1];
colorbar

Fill Area Between Contours

Fill the area between contours by setting the Fill input of fcontour to 'on'. If you want interpolated shading instead, use the fsurf function with its option 'EdgeColor' set to 'none' followed by the command view(0,90).

Create a plot that looks like a sunset by filling the contours of

$$erf((y+2{)}^3)-e^{(-0.65((x-2{)}^2+(y-2{)}^2)}.$$

syms x y
f = erf((y+2)^3) - exp(-0.65*((x-2)^2+(y-2)^2));
fcontour(f,'Fill','on')

Specify Levels for Contour Lines

Set the values at which fcontour draws contours by using the 'LevelList' option.

syms x y
f = sin(x) + cos(y);
fcontour(f,'LevelList',[-1 0 1])

Control Resolution of Contour Lines

Control the resolution of contour lines by using the 'MeshDensity' option. Increasing 'MeshDensity' can make smoother, more accurate plots while decreasing it can increase plotting speed.

Divide a figure into two using subplot. In the first subplot, plot the contours of $$\sin (x)\sin (y)$$. The corners of the squares do not meet. To fix this issue, increase 'MeshDensity' to 200 in the second subplot. The corners now meet, showing that by increasing 'MeshDensity' you increase the plot's resolution.

syms x y
subplot(2,1,1)
fcontour(sin(x).*sin(y))
title('Default MeshDensity = 71')

subplot(2,1,2)
fcontour(sin(x).*sin(y),'MeshDensity',200)
title('Increased MeshDensity = 200')

Add Title and Axis Labels and Format Ticks

Plot $$x\sin (y)-y\cos (x)$$. Add a title and axis labels. Create the x-axis ticks by spanning the x-axis limits at intervals of pi/2. Display these ticks by using the XTick property. Create x-axis labels by using arrayfun to apply texlabel to S. Display these labels by using the XTickLabel property. Repeat these steps for the y-axis.

To use LaTeX in plots, see latex.

syms x y
fcontour(x*sin(y)-y*cos(x), [-2*pi 2*pi])
grid on
title('xsin(y)-ycos(x) for -2\pi < x < 2\pi and -2\pi < y < 2\pi')
xlabel('x')
ylabel('y')
ax = gca;

S = sym(ax.XLim(1):pi/2:ax.XLim(2));
ax.XTick = double(S);
ax.XTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false);

S = sym(ax.YLim(1):pi/2:ax.YLim(2));
ax.YTick = double(S);
ax.YTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false);

Create Animations

Create animations by changing the displayed expression using the Function property of the function handle, and then using drawnow to update the plot. To export to GIF, see imwrite.

By varying the variable i from –π/8 to π/8, animate the parametric curve isin(x) + icos(y).

syms x y
fc = fcontour(-pi/8.*sin(x)-pi/8.*cos(y));
for i=-pi/8:0.01:pi/8
    fc.Function = i.*sin(x)+i.*cos(y);
    drawnow
		pause(0.05)
end

Input Arguments

f — Expression or function to be plotted

symbolic expression | symbolic function

Expression or function to be plotted, specified as a symbolic expression or function.

[min max] — Plotting range for x and y

[–5 5] (default) | vector of two numbers

Plotting range for x and y, specified as a vector of two numbers. The default range is [-5 5].

[xmin xmax ymin ymax] — Plotting range for x and y

[–5 5 –5 5] (default) | vector of four numbers

Plotting range for x and y, specified as a vector of four numbers. The default range is [-5 5 -5 5].

ax — Axes object

axes object

Axes object. If you do not specify an axes object, then the plot function uses the current axes.

LineSpec — Line style and color

character vector | string

Line style and color, specified as a character vector or string containing a line style specifier, a color specifier, or both.

Example: '--r' specifies red dashed lines

These two tables list the line style and color options.

Line Style Specifier	Description
-	Solid line (default)
--	Dashed line
:	Dotted line
-.	Dash-dot line

Color Specifier	Description
y	yellow
m	magenta
c	cyan
r	red
g	green
b	blue
w	white
k	black

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'MeshDensity',30

The properties listed here are only a subset. For a complete list, see FunctionContour Properties.

MeshDensity — Number of evaluation points per direction

71 (default) | number

Number of evaluation points per direction, specified as a number. The default is 71. Because fcontour uses adaptive evaluation, the actual number of evaluation points is greater.

Example: 30

Fill — Fill between contour lines

'off' (default) | on/off logical value

Fill between contour lines, specified as 'on' or 'off', or as numeric or logical 1 (true) or 0 (false). A value of 'on' is equivalent to true, and 'off' is equivalent to false. Thus, you can use the value of this property as a logical value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.

• A value of 'on' fill the spaces between contour lines with color.

• A value of 'off' leaves the spaces between the contour lines unfilled.

LevelList — Contour levels

vector of z values

Contour levels, specified as a vector of z values. By default, the fcontour function chooses values that span the range of values in the ZData property.

Setting this property sets the associated mode property to manual.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

LevelListMode — Selection mode for LevelList

'auto' (default) | 'manual'

Selection mode for the LevelList, specified as one of these values:

• 'auto' — Determine the values based on the ZData values.

• 'manual' — Use manually specified values. To specify the values, set the LevelList property. When the mode is 'manual', the LevelList values do not change if you change the Function property or the limits.

LevelStep — Spacing between contour lines

0 (default) | scalar numeric value

Spacing between contour lines, specified as a scalar numeric value. For example, specify a value of 2 to draw contour lines at increments of 2. By default, LevelStep is determined by using the ZData values.

Setting this property sets the associated mode property to 'manual'.

Example: 3.4

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

LevelStepMode — Selection mode for LevelStep

'auto' (default) | 'manual'

Selection mode for the LevelStep, specified as one of these values:

• 'auto' — Determine the value based on the ZData values.

• 'manual' — Use a manually specified value. To specify the value, set the LevelStep property. When the mode is 'manual', the value of LevelStepMode does not change when the Function property or the limits change.

LineColor — Color of contour lines

'flat' (default) | RGB triplet | hexadecimal color code | 'r' | 'g' | 'b' | ...

Color of contour lines, specified as 'flat', an RGB triplet, a hexadecimal color code, a color name, or a short name. To use a different color for each contour line, specify 'flat'. The color is determined by the contour value of the line, the colormap, and the scaling of data values into the colormap. For more information on color scaling, see Control Colormap Limits.

To use the same color for all the contour lines, specify an RGB triplet, a hexadecimal color code, a color name, or a short name.

For a custom color, specify an RGB triplet or a hexadecimal color code.

• An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1], for example, [0.4 0.6 0.7].

• A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Therefore, the color codes "#FF8800", "#ff8800", "#F80", and "#f80" are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.

Color Name	Short Name	RGB Triplet	Hexadecimal Color Code	Appearance
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"
"none"	Not applicable	Not applicable	Not applicable	No color

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB^® uses in many types of plots.

RGB Triplet	Hexadecimal Color Code	Appearance
[0 0.4470 0.7410]	"#0072BD"
[0.8500 0.3250 0.0980]	"#D95319"
[0.9290 0.6940 0.1250]	"#EDB120"
[0.4940 0.1840 0.5560]	"#7E2F8E"
[0.4660 0.6740 0.1880]	"#77AC30"
[0.3010 0.7450 0.9330]	"#4DBEEE"
[0.6350 0.0780 0.1840]	"#A2142F"

LineStyle — Line style

"-" (default) | "--" | ":" | "-." | "none"

Line style, specified as one of the options listed in this table.

Line Style	Description	Resulting Line
"-"	Solid line
"--"	Dashed line
":"	Dotted line
"-."	Dash-dotted line
"none"	No line	No line

LineWidth — Line width

0.5 (default) | positive value

Line width, specified as a positive value in points, where 1 point = 1/72 of an inch. If the line has markers, then the line width also affects the marker edges.

The line width cannot be thinner than the width of a pixel. If you set the line width to a value that is less than the width of a pixel on your system, the line displays as one pixel wide.

Output Arguments

fc — One or more function contour objects

scalar | vector

One or more function contour objects, returned as a scalar or a vector. These objects are unique identifiers, which you can use to query and modify the properties of a specific contour plot. For details, see FunctionContour Properties.

Algorithms

fcontour assigns the symbolic variables in f to the x axis, then the y axis, and symvar determines the order of the variables to be assigned. Therefore, variable and axis names might not correspond. To force fcontour to assign x or y to its corresponding axis, create the symbolic function to plot, then pass the symbolic function to fcontour.

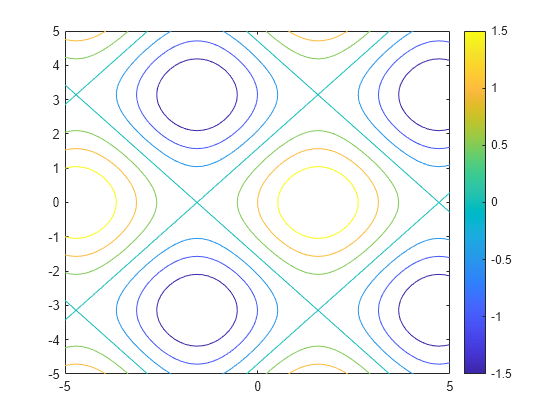
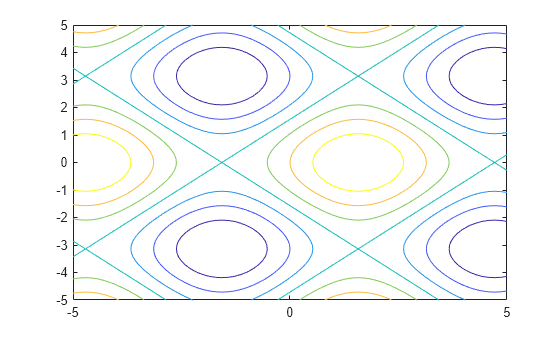
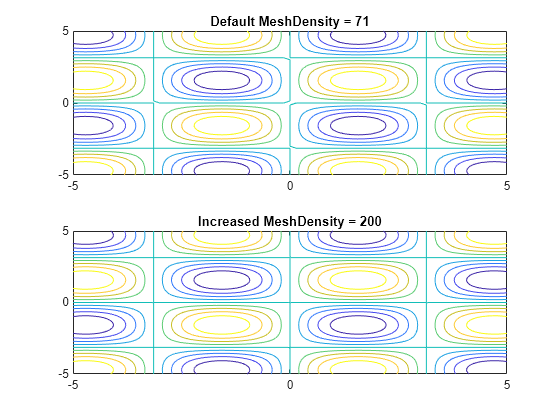
For example, the following code plots the contour of the surface f(x,y) = sin(y) in two ways. The first way forces the waves to oscillate with respect to the y axis. The second way assigns y to the x axis because it is the first (and only) variable in the symbolic function.

syms x y;
f(x,y) = sin(y);

figure;
subplot(2,1,1)
fcontour(f);
subplot(2,1,2)
fcontour(f(x,y)); % Or fcontour(sin(y));

Version History

Introduced in R2016a