基于机理和模型的特征提取与预测性维护
作者 : 刘海伟、MathWorks
随着数据科学的发展,越来越多的领域工程师希望将人工智能算法用于预测性维护,例如使用机器学习或深度学习算法训练模型,用于状态监控,异常检测或寿命预测。通常我们寄希望于通过传感器能够直接计算得到一些统计和信号特征作为健康指标,用于模型训练。但对于工程领域,很多设备正常运行本身就会涉及到不同的工况,不同的参数设置,使得所采集的传感器数据(或通过其计算的特征)也是一直有变化的(这种变化正是设备本身的物理机理的表现),因此很多情况无法单纯通过传感器的统计和信号特征来预测健康状况。本文试图提供一些思路,可以结合机理模型进行特征提取来用于健康诊断。
本文含以下章节(约3600字)。
1. 简单示例
通过信号处理或统计分析来进行特征提取
基于模型或机理本身来进行特征提取
2. 离心泵
构建泵的机理模型
故障监测思路和方法
3. 无级变速箱
物理机理系统
仿真生成数据
在线参数估计
估计参数与设计参数对比与验证
1. 简单示例
为了方便理解,我们先看个简单的示例。例如我们有两类加速度数据,分别是正常数据和故障数据。接下来,我们会按这个顺序进行分析:
1. 通过统计特征和信号特征尝试分类
2. 通过拟合模型得到的参数作为特征进行分类
通常我们可能首先想到通过信号处理或统计分析来进行特征提取。
例如我们通过统计直方图看看故障数据相比正常数据是否发生均值偏移或分布变化。
简单看来,这两个分布还是很相似的,这并不是个有区分度的特征(这个区分度我们可以用方差分析ANOVA方法进行量化)。
接下来我们可以从信号分析角度看看在频域上是否有一些可以用来进行分类的特征。我们使用频谱估计得到功率谱密度估计。同样,功率谱密度反映出来的信息(包括峰值对应的频率,峰值的大小,频域带宽)并没有明显的不同。因此这说明频域上也找不到一个好的特征。
这种情况下我们可以考虑基于模型或机理本身来进行特征提取。
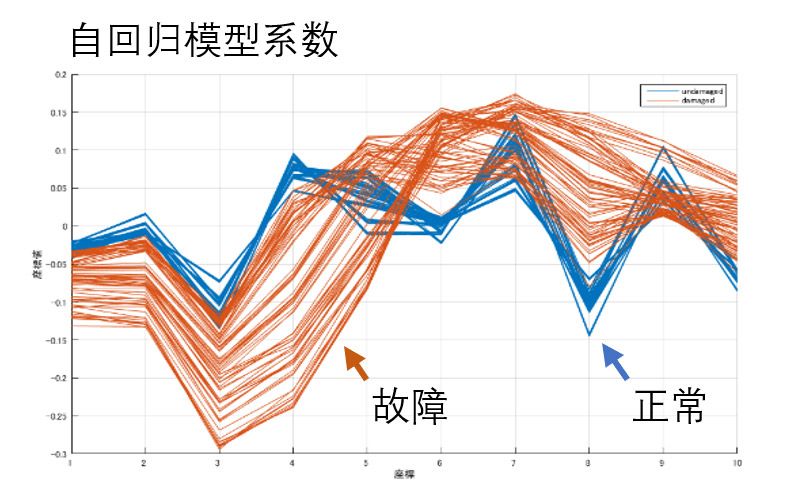
例如,假设我们对这个系统比较清楚,提前知道这是一个自回归系统
\[y(t)+a_1y(t-1)+...+a_{na} y(t-na) = e(t), \]
其中\(y(t)\) 是输出,\(e(t)\) 是白噪音扰动,我们则可以通过系统辨识的方法,利用已有的数据对模型的系数\(a_{ni} \)进行参数估计,可以对两类(正常和故障)数据分片进行估计得到很多分片的结果。发现正常数据和故障数据对应模型的各阶系数\(a_{ni} \) 区别度比较高。因此可以将\(a_{ni} \) 作为特征给到机器学习算法用于训练。结合系统机理可以在少量数据的情况下得到相对精准的模型。
2. 离心泵
接下来我们针对一个工程领域实际设备来看看对于如何结合机理模型进行特征提取。我们在这个示例中的思路正如开始提到的,不会直接使用采集到的传感器数据进行模型训练,而是先进行机理模型拟合(例如拟合Euler方程的系数),得到模型系数作为特征,然后再进行故障分析。
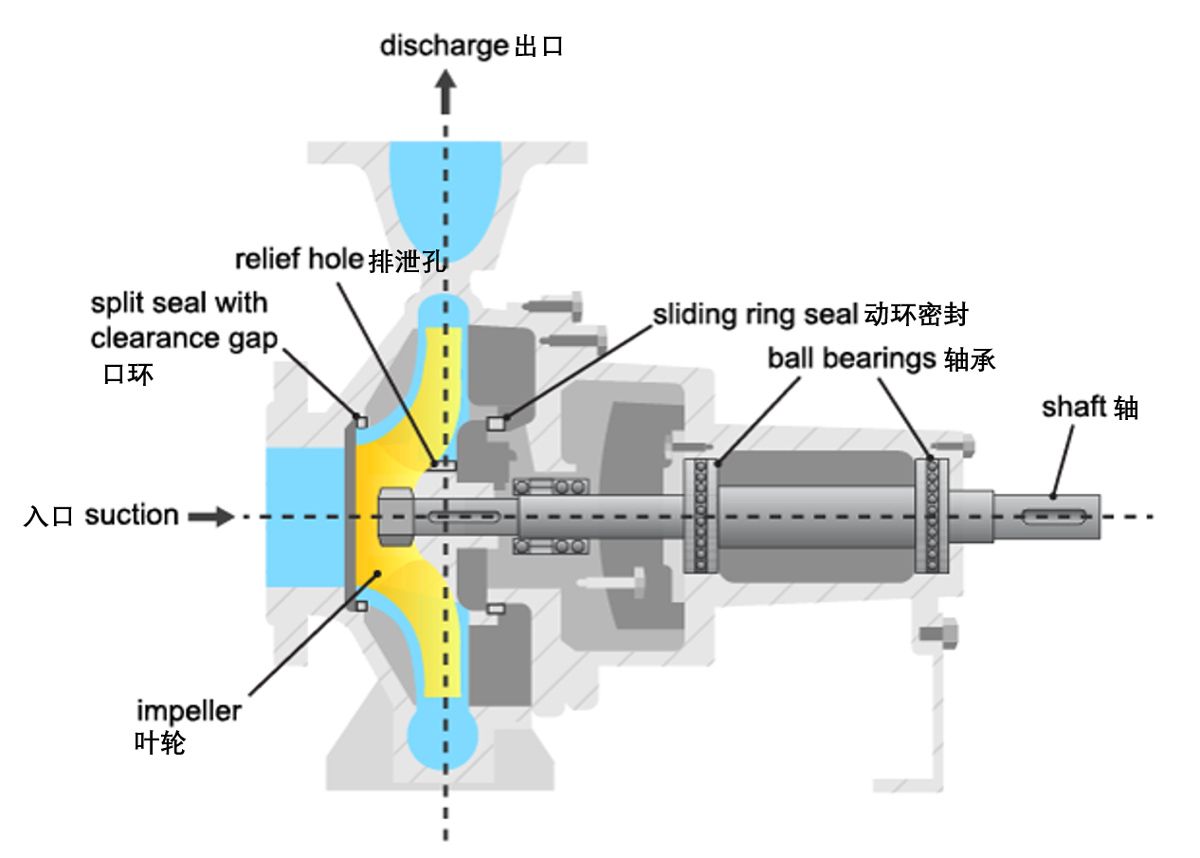
离心泵经常会有液压件或机械件的损坏。最常见的部件损坏像动环密封,滚动轴承,另外像叶轮叶片破损,驱动电机故障也很常见。在这个例子中我们尝试从机理模型入手,提取能够进行故障诊断或预测的特征。
我们的传感器可以测得的量有:
- 入口和出口的压力差\(\Delta p \)
- 转速\(\omega \)
- 电机扭矩\(M_{mot} \) 和泵扭矩\(M_p \)
- 泵的出口流量\(\mathcal Q \)
构建泵的机理模型:
理想状况下,由Euler方程我们可以得到
\[H_{th}=h_1ω^2 − h_2 ωQ \]
其中, \(H_{th} = \frac {\Delta p}{ρg} \) 是理论扬程,单位是米。\(h_1\), \(h_2\)是比例系数
如果考虑摩擦,非切向流速引起的接触损失,实际扬程可以表示为:
\[H = h_{nn}ω_2 − h_{nv}\omega Q − h_{vv}Q^2 \]
其中 \(h_{nn}\), \(h_{nv}\) 和 \(h_{vv}\) 是比例系数,可以参看作模型参数。
同样对于泵的扭矩
\[M_P = \mathit ρg (h_{nn}\omega Q - h_{nv}Q^2 - h_{vv}\frac{Q^3}{\omega }) \]
故障监测思路和方法:
本示例中我们主要通过参数估计的方法进行故障监测。主要思路是利用健康运行数据估计机理模型参数(上述方程中的 \(h_{nn}, h_{nv}, h_{vv} \))以及他们的不确定度。接下来对测试数据同样进行机理模型的参数估计,得到新的参数(\(h_{nn}, h_{nv}, h_{vv} \))并与健康数据估计出来的模型参数进行比较来看是否偏离健康状态。
本示例中用的数据为稳态数据,泵以恒定速度运行,并测得扬程和出口流量。通过不断改变出口阀门流量,测得对应的扬程值,得到Q-H曲线。
我们可以简化扬程方程和扭矩方程为:
\[H \approx h_{nn}\omega ^2 − h_{nv}\omega \mathcal Q − h_{vv}\mathcal Q^2 \]
\[M_{p} \approx k_{0}ωQ − k_{1}Q^2 + k_{2}ω^2 \]
其中,\(h_{nn},h_{nv},h_{vv},k_{0},k_{1},k_{2} \)即为我们要估计的参数。接下来,我们通过曲线拟合的方法,将动力学方程的系数计算出来。通过测量我们可以得到\(ω, Q, H\) and \(M_{p} \), 对于上述参数则可以通过线性最小二乘即可得到。
计算方程系数:
可以先计算三种设备状况下(健康,大间隙,小间隙)方程的系数,查看系数是否会因为故障发生变化
我们会得到对应三种状况的参数值。我们以扬程方程对应的hnn,hnv,hvv的结果为例:
结果显示hnn的值会随密封间隙变大而变小,hvv的值会随密封间隙变大而变大。同样对于扭矩方程对应的\(k_{0},k_{1},k_{2} \)同样可以得到相应的结果。
计算不确定度:
前面初步分析可以得到一个粗略结果,即系数的变化可以反映故障。然而,即使对于健康的设备,因为测量误差,液体成分和粘度变化以及驱动电机的扭矩特性都会导致测量值的波动。这些波动会引入参数的不确定度。
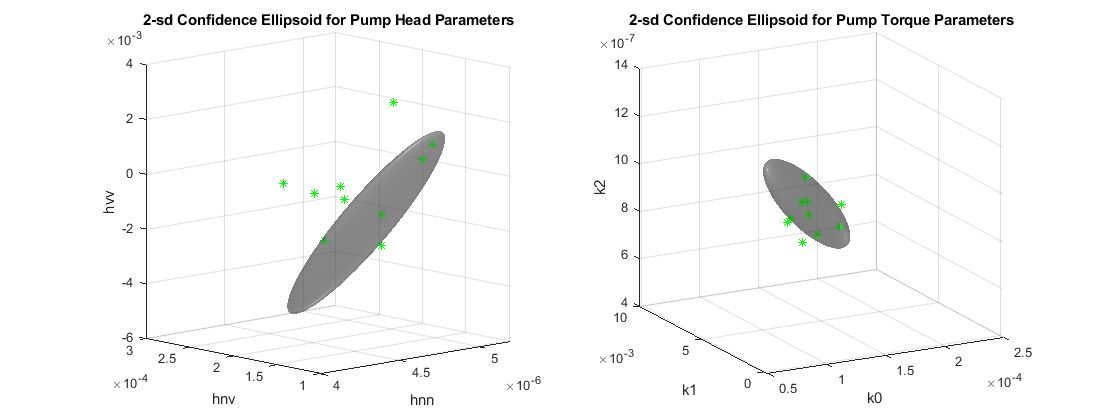
因此我们会在健康设备上做很多组实验,并进行参数估计,得到结果之后计算这些结果的均值和方差(因为此处为多维数组,对扬程参数来说是三维\(h_{nn},h_{nv},h_{vv} \)对扭矩参数来说同样是三维\(k_{0},k_{1},k_{2} \),因此用协方差矩阵)
根据结果可视化参数均值和2倍标准差对应的置信区间
基于置信区间量化异常:
为了量化测试数据通过参数估计得到的结果\((h_{nn},h_{nv},h_{vv},k_{0},k_{1},k_{2} \))与健康系数值的差距(距离),我们使用马氏距离:
如果我们在74%置信边界(对应2倍标准差)对应的结果为健康系数的边界,ParDist中大于2^2 = 4的都要标记为异常值,也就是故障设备。
通过one-class分类器量化异常:
在没有故障标签,只有健康数据的情况下,我们可以使用一分类学习器训练数学模型。在这个场景中,先对扬程方程的系数进行训练,我们选择重要的两个指标参数\(h_{nn} \) 和\(h_{vv} \) 作为预测变量:
一分类的SVM的模型结果中,值为0的等高线即为健康与故障的分界线。异常点用红色的圈标识。同样对于扭矩方程,我们选择\(k_{0},k_{2} \)作为预测变量,同样可以监测异常值(红圈对应的数据)。


接下来我们可以实现故障分类,同样可以先进行参数辨识。之后可以使用统计方法例如最大似然假设检验或者机器学习的分类算法例如集成树等实现故障分类。该示例的完整内容请参考帮助文档(Fault Diagnosis of Centrifugal Pumps Using Steady State Experiments)
上述这个示例中我们用的稳态运行数据,并用来对一个设备的稳态模型进行辨识,从而提取表征模型运行状态指标的参数。
3. 无级变速箱(CVT)
接下来我们再看一个动态模型的例子。对于动态系统,测量信号(输出)的变化通常是由于系统的输入信号的变化导致的。我们可以通过输入输出辨识出系统参数。同时我们也可以使用系统辨识工具箱一些递归估计函数来对实时数据进行动态参数估计,从而得到系统状态指标的变化趋势用于指导对系统健康状况的判断。
物理机理系统:
该系统是一个液压阀驱动的无级变速箱(CVT)[1], 阀门压力连接到CVT可以用来改变速比并将发动机扭矩传输到车轮。阀门的输入输出可以近似为:
\[y(t)=k(t)u(t)+b(t) \]
其中\(\frac{-b(t)}{k(t)} \lt u \le 1 \)
t是当前时间,\(y(t)\)是阀门压力,\(u(t)\)是[0,1]范围的无量纲输入。
斜率\(k(t)\),补偿\(b(t)\)会随系统温度变化而变化。因此现在我们希望通过测得的\(y(t)\),\(u(t)\)来实时估计\(k(t)\),\(b(t)\),从而对系统有一个理解并与正向设计的\(k(t)\),\(b(t)\)的值进行比对,查看系统是否正常运行。
仿真生成数据:
我们先设计真实的斜率和补偿值为:在 t=0s,k(0)=70,b(0)=-15。在t=50s时发动机启动。参数一直随时间变化直到t=950s,此时 k(950)=50,b(950)=-13。采样时间Ts=0.1s。接下来我们设计输入量u(t)
- t=0s到t=50s,
- t=50s 到t=950s,每100s更新一次,分别是 0.40, 0.45, 0.50, 0.55, 0.60, 0.55, 0.50, 0.45, 0.40,并加上一个高斯噪声。
于是我们得到的系统方程为
\[y(t)=k(t)u(t)+b(t)+e(t) \]

在线参数估计:
实际的系统运行中,我们通常只能测得\(u(t)\),\(y(t)\),我们可以使用在线参数估计得一些算法,例如递归最小二乘,实现对模型系数实时求解,从而得到对应的\(k(t)\),\(b(t)\)。
先向量化我们的设计模型:
\[y(t)=k(t)u(t)+b(t)+e(t) \] \[=[k(t) b(t)][u(t) 1]^T+e(t) \] \[=H(t)x(t)+e(t) \]
其中\(H(t)=[k(t) b(t)] \)即为我们要估计得参数。我们使用recursiveLS函数用于在线参数估计。使用step函数,可以根据输入\(x(t)\)和输出\(y(t)\)来更新参数\(H(t)\)。
估计参数与设计参数对比与验证
可视化参数估计的结果\((k(t),b(t))\),来与设计值进行比对。

这个例子主要还是使用运行数据进行参数估计,辨识出的参数,例如本例中的,\(k(t)\),\(b(t)\)用来作为描述系统健康状态的特征指标,既可以与设计值比较,也可以通过参数的变化趋势来进行故障诊断,例如,针对系统参数识别系统的突然变化(详见Detect Abrupt System Changes Using Identification Techniques)。
2022 年发布