フーリエ変換とは?
フーリエ変換は、データ解析手法のひとつで、一般的には時間領域のデータを周波数領域へ変換するためのアルゴリズムとして利用されます。信号処理の分野においては、周波数解析手法として、スペクトル解析に用いられる重要な技術です。
フーリエ級数展開とフーリエ変換
ある周期信号をsinとcosの成分の和として表したのが、フーリエ級数展開です。


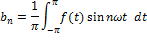
この式は、オイラーの公式
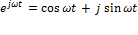
を用いることにより、以下の様に書き換えることができます。これを、複素フーリエ級数と呼びます。


フーリエ変換は、この複素フーリエ級数を、非周期信号へ拡張したものと考えられます。以下に、フーリエ変換の定義式を示します。

フーリエ変換により、変換前の信号の周波数成分の分布を知ることができます。つまり、フーリエ変換は、物理的には「時間領域の信号から周波数領域の信号への変換」という意味となります。フーリエ変換の逆処理である、逆フーリエ変換(フーリエ逆変換)の定義式は、

離散フーリエ変換
フーリエ変換の対象のデータが離散値である場合を特に、”離散フーリエ変換(DFT: Discrete Fourier Transform)”と呼びます。以下に、離散フーリエ変換の定義式と変換イメージを示します。

DFTの定義式と変換イメージ
高速フーリエ変換
上記定義式を見ると分かるように、離散フーリエ変換の処理においては、一点のデータを得るために多くの積和演算を必要とするため、変換対象データの増大に伴う膨大な演算時間が問題となるケースがあります。離散フーリエ変換の内部処理で繰り返される演算の相似性に着目し、データ点数に制約を与えることで変換処理の高速化を実現したのが、高速フーリエ変換(FFT: Fast Fourier Transform)です。FFTの逆処理を、逆高速フーリエ変換(IFFT: Inverse Fast Fourier Transform)と言います。例として、50[Hz]の正弦波、三角波、矩形波、のこぎり波それぞれに対して、FFT処理を行った結果を以下に示します。

各種波形のFFT処理結果
周波数領域において、三角波と矩形波は、基本波(左端:50[Hz])に対する奇数高調波成分(150[Hz], 250[Hz], …)、のこぎり波は偶数と奇数高調波成分(100[Hz], 150[Hz], 200[Hz], …)が存在することが分かります。
高速フーリエ変換の目的・応用例
高速フーリエ変換は、音声処理や画像処理等の典型的な信号処理アプリケーションから、制御、地学、医療等、非常に幅広い分野にわたり、主に周波数解析をベースとした目的に用いられます。以下はその応用例です。
- 生体信号の周期性に着目した疾病の事前検知
- 各種気象データを用いた災害予知
- 時間軸測定器による周波数分析
- プラント設備、橋梁等の健全性のモニタリング
- 楽器のチューニング
近年のディジタル通信における変調方式の主流である、直行周波数分割多重(OFDM: Orthogonal Frequency Division Multiplexing)においては、サブキャリア間で干渉しないマルチキャリア信号を算術的に得るためにIFFT演算が適用されています。さらに、時間軸領域での畳み込み演算は、周波数領域では乗算に相当するという性質を応用し、フィルタリング処理の様に畳み込み演算を多用するケースでは、対象信号とフィルタ係数をFFTにより一旦周波数領域へ変換してから乗算処理を行い、その後IFFT処理で時間領域へ戻すという手順を踏むことにより、フィルタリングがより高速に行えることが知られています。
実際の高速フーリエ変換処理・プログラミング記述
プログラミング環境等によりフーリエ変換処理を実現する際には、FFT演算だけでなく、周波数シフト等の前処理や、振幅・位相成分の抽出、縦軸/横軸のスケーリング、各種描画機能等の後処理が重要となります。以下のリストは、MATLAB®が提供する、フーリエ変換関連の代表的な関数例です。これらの関数には、詳細なドキュメントや、使用法の例題・サンプルプログラム等も用意されており、さらに、MATLABの2次元・3次元系の豊富な描画機能を組み合わせることで、フーリエ変換をベースとした基本的なスペクトル解析を容易に実現することができます。
また、MATLAB®のオプション製品である、Signal Processing Toolbox™を使用することにより、容易に種々のスペクトル解析を実現することができます。
製品使用例および使い方
その他製品に関する情報
参考: MATLAB/Simulinkを使ってみませんか? - 信号処理編, 体験セミナー - ディジタル信号処理コース, 具体例で学ぶ信号処理ワークフロー ~すぐに使えるテクニック:実践編~
