El concepto de pendiente o inclinación de una función recta es muy intuitivo para cualquier persona. Desde el punto de vista matemático, la pendiente indica cuánto se incrementa o decrementa la función y = f(x) al incrementar el valor de la variable x. Matemáticamente,
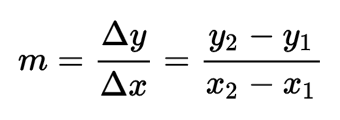
Sin embargo, ¿cuál es la pendiente en las funciones que no son rectas? Obviamente, la pendiente será distinta en cada punto de la función. Por lo tanto, podríamos obtener otra función f'(x) que, para cada punto x, nos indicase el valor de la pendiente en la función f(x) original. A esta función se le conoce como función derivada o derivada. La derivada se define matemáticamente como la pendiente de la recta tangente a la función f(x) cuando nos aproximamos al punto x.
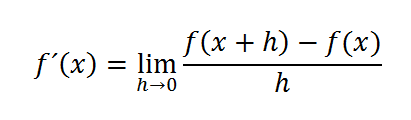
Cuando tenemos funciones conocidas, es fácil calcular la derivada a partir de unas reglas de derivación. Pero, ¿y si no conocemos la función? ¿y si tenemos una señal ruidosa y aleatoria, o la mezcla de varias funciones desconocidas? En estos casos, podemos calcular la derivada (es decir, el límite) de forma aproximada, tomando un valor de h pequeño.
En este problema, debes calcular el vector derivada dv de un vector v y un tamaño de paso h como parámetros de entrada.
Solution Stats
Problem Comments
Solution Comments
Show commentsProblem Recent Solvers31
Suggested Problems
-
21019 Solvers
-
5970 Solvers
-
208 Solvers
-
719 Solvers
-
1391 Solvers
More from this Author1
Problem Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!