ismaxphase
Verify that discrete-time filter System object is maximum phase
Syntax
Description
flag = ismaxphase(___,Arithmetic=arithType)arithType input
using either of the previous syntaxes.
For more input options, see ismaxphase in Signal Processing Toolbox™.
Examples
Design an allpass filter and determine if the filter has maximum phase.
Using the dsp.AllpassFilter System object™, design an allpass filter that uses the minimum multiplier structure.
a = dsp.AllpassFilter
a =
dsp.AllpassFilter with properties:
Structure: 'Minimum multiplier'
AllpassCoefficients: [-0.7071 0.5000]
TrailingFirstOrderSection: false
Using the ismaxphase function, determine if the filter has maximum phase.
ismaxphase(a)
ans = logical
1
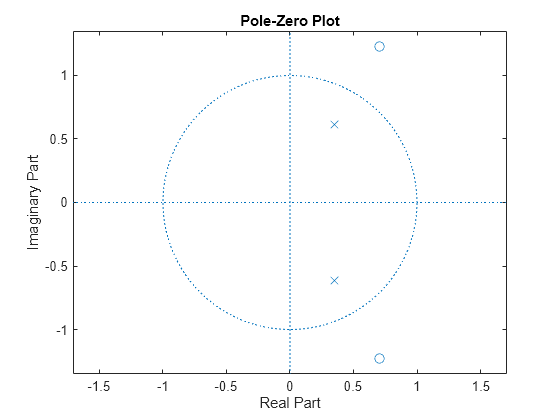
Verify the location of poles and zeros of the filter transfer function on the z-plane. By definition, the zeros of the maximum phase filter must be outside the unit circle.
zplane(a)
Input Arguments
Tolerance value to determine when two numbers are close enough to be considered
equal, specified as a positive scalar. If not specified, tol
defaults to eps^(2/3).
Arithmetic used in the filter analysis, specified as 'double',
'single', or 'Fixed'. When the arithmetic
input is not specified and the filter System object is unlocked, the analysis tool assumes a double-precision filter. When the
arithmetic input is not specified and the System object is locked, the function performs the analysis based on the data type of
the locked input.
The 'Fixed' value applies to filter System objects with fixed-point
properties only.
When the 'Arithmetic' input argument is specified as
'Fixed' and the filter object has the data type of the
coefficients set to 'Same word length as input', the arithmetic
analysis depends on whether the System object is unlocked or locked.
unlocked –– The analysis object function cannot determine the coefficients data type. The function assumes that the coefficients data type is signed, has a 16-bit word length, and is auto scaled. The function performs fixed-point analysis based on this assumption.
locked –– When the input data type is
'double'or'single', the analysis object function cannot determine the coefficients data type. The function assumes that the data type of the coefficients is signed, has a 16-bit word length, and is auto scaled. The function performs fixed-point analysis based on this assumption.
To check if the System object is locked or unlocked, use the isLocked function.
When the arithmetic input is specified as 'Fixed' and the filter
object has the data type of the coefficients set to a custom numeric type, the object
function performs fixed-point analysis based on the custom numeric data type.
Output Arguments
Flag to determine if the filter has maximum phase, returned as a logical:
1–– Filter has maximum phase.0–– Filter has non maximum phase.
Data Types: logical
More About
A causal and stable discrete-time system is said to be strictly maximum-phase when all its zeros are outside the unit circle. A causal and stable LTI system is a maximum-phase system if its inverse is causal and unstable.
Such a system is called a maximum-phase system
because it has the maximum group delay (grpdelay) of the set of systems that have the same magnitude response.
Version History
Introduced in R2013aStarting in R2024b, the ismaxphase analysis function supports the
dsp.VariableFIRDecimator and dsp.VariableFIRInterpolator objects.
The dsp.BiquadFilter object issues a warning and will be removed in a
future release. Use the dsp.SOSFilter object
instead. For more information on how to replace your existing code, see the
Compatibility Considerations section in the dsp.BiquadFilter reference page.
Starting in R2024b, this function supports the dsp.DCBlocker object.
Starting in R2023b, the ismaxphase analysis function supports the
dsp.ParallelFilter
and the dsp.Delay objects.
The dsp.BiquadFilter object will be removed in a future release. Use
the dsp.SOSFilter object
instead.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)